题目内容
11.有两件事和四个图象,两件事为:①我离开家不久,发现自己把作业本忘在家里了,于是返回家找到作业本再上学;②我出发后,心情轻松,缓缓前行,后来为了赶时间开始加速,四个图象如下: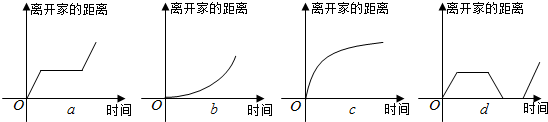
与事件①,②对应的图象分别为( )
| A. | a,b | B. | a,c | C. | d,b | D. | d,c |
分析 由实际背景出发确定图象的特征,从而解得.
解答 解:①我离开家不久,发现自己把作业本放在家里了,于是立刻返回家里取了作业本再上学,中间有回到家的过程,故d成立;
②我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速,故b成立.
故选:C.
点评 本题考查的知识点是函数的图象,我们分析实际情况中离家距离随时间变化的趋势,找出关键的图象特征,对四个图象进行分析,即可得到答案.

练习册系列答案
相关题目
1.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤0}\\{{x}^{3}-3x,x>0}\end{array}\right.$,若直线y=kx-$\frac{1}{4}$与f(x)的图象有三个公共点,则实数k的取值范围是( )
| A. | (-$\frac{9}{4}$,+∞) | B. | (0,+∞) | C. | (-$\frac{7}{4}$,+∞) | D. | (-3,-$\frac{9}{4}$)∪(-$\frac{7}{4}$,+∞) |
19.已知△ABC的内角A,B,C的对边分别为a,b,c,若$\sqrt{3}$acosC+($\sqrt{3}$c-2b)cosA=0,且cosA•cosC=$\frac{\sqrt{3}}{4}$,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
6.已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.则下列条件中一定能使得l1∥l2成立的是( )
| A. | m=4 | B. | m=0 | C. | m=4或m=-4 | D. | m=4且n≠-2 |
16.在等比{an}数列中,a2a6=16,a4+a8=8,则$\frac{{a}_{20}}{{a}_{10}}$=( )
| A. | 1 | B. | -3 | C. | 1或-3 | D. | -1或3 |
3.已知向量$\overrightarrow{CA}$,$\overrightarrow{CB}$,满足|$\overrightarrow{CA}$|=1,∠ACB=$\frac{π}{2}$,若关于实数x的函数f(x)=|x$\overrightarrow{CA}$+2$\overrightarrow{CB}$|-|$\overrightarrow{CB}$$+\overrightarrow{CA}$|,有唯一的零点,已M为AB的中点,则$\overrightarrow{MA}$$•\overrightarrow{MB}$=( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{4}{9}$ | D. | -1 |