题目内容
9.$\sqrt{{a}^{\frac{11}{2}}\sqrt{{a}^{-3}}}$-3${\;}^{-lo{g}_{3}2}$+log${\;}_{\sqrt{3}}$1=a2-$\frac{1}{2}$.分析 根据指数幂的运算性质的法则计算即可.
解答 解:$\sqrt{{a}^{\frac{11}{2}}\sqrt{{a}^{-3}}}$-3${\;}^{-lo{g}_{3}2}$+log${\;}_{\sqrt{3}}$1=$({a}^{\frac{11}{2}}•{a}^{-\frac{3}{2}})^{\frac{1}{2}}$-$\frac{1}{2}$+0=a2-$\frac{1}{2}$,
故答案为:a2-$\frac{1}{2}$.
点评 本题考查了指数幂的运算性质,属于基础题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.已知($\frac{1}{2}$)sin2θ<1,则θ是( )
| A. | 第一或第二象限的角 | B. | 第二或第四象限的角 | ||
| C. | 第一或第三象限的角 | D. | 第二或第三象限的角 |
1.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤0}\\{{x}^{3}-3x,x>0}\end{array}\right.$,若直线y=kx-$\frac{1}{4}$与f(x)的图象有三个公共点,则实数k的取值范围是( )
| A. | (-$\frac{9}{4}$,+∞) | B. | (0,+∞) | C. | (-$\frac{7}{4}$,+∞) | D. | (-3,-$\frac{9}{4}$)∪(-$\frac{7}{4}$,+∞) |
19.已知△ABC的内角A,B,C的对边分别为a,b,c,若$\sqrt{3}$acosC+($\sqrt{3}$c-2b)cosA=0,且cosA•cosC=$\frac{\sqrt{3}}{4}$,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
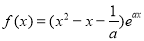 (
(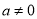 ).
).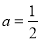 时,求函数
时,求函数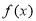 的零点;
的零点;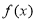 的单调区间;
的单调区间;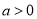 时,若
时,若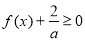 对
对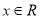 恒成立,求
恒成立,求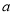 的取值范围.
的取值范围.