题目内容
9.sin22°30′•cos22°30′的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据题意,将原式恒等变形可得sin22°30′•cos22°30′=$\frac{1}{2}$(2sin22°30′•cos22°30′)=$\frac{1}{2}$sin(2×22°30′)=$\frac{1}{2}$sin45°,由特殊角的三角函数值计算可得答案.
解答 解:根据题意,sin22°30′•cos22°30′=$\frac{1}{2}$(2sin22°30′•cos22°30′)=$\frac{1}{2}$sin(2×22°30′)=$\frac{1}{2}$sin45°=$\frac{\sqrt{2}}{4}$;
故选:B.
点评 本题考查正弦的二倍角公式,解题的关键是熟悉二倍角公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知△ABC的内角A,B,C的对边分别为a,b,c,若$\sqrt{3}$acosC+($\sqrt{3}$c-2b)cosA=0,且cosA•cosC=$\frac{\sqrt{3}}{4}$,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
18.-90°+k•360°(k∈z)表示的是( )
| A. | 第一象限角 | B. | 第三象限角 | C. | 界限角 | D. | 第四象限角 |
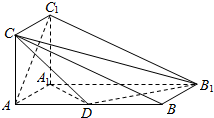 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.