题目内容
直线与双曲线位置关系的判定及应用
已知双曲线C的方程为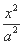 -
-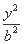 =1(a>0,b>0),离心率e=
=1(a>0,b>0),离心率e=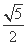 ,顶点到渐近线的距离为
,顶点到渐近线的距离为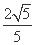 .
.
(1)求双曲线C的方程;
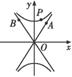
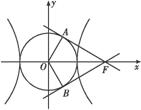
(2)如图,P是双曲线C上一点,A、B两点在双曲线C的两条渐近线上,且分别位于第一、二象限.
若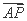 =λ
=λ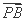 ,λ∈
,λ∈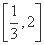 .求△AOB的面积的取值范围.
.求△AOB的面积的取值范围.
解:(1)由题意知,双曲线C的顶点(0,a)到渐近线ax-by=0的距离为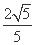 ,
,
∴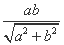 =
=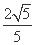 ,即
,即 =
=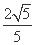 .
.
由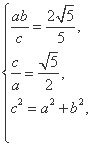 得
得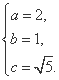
∴双曲线C的方程为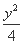 -x2=1.
-x2=1.
(2)由(1)知双曲线C的两条渐近线方程为y=±2x,
设A(m,2m),B(-n,2n),m>0,n>0.
由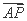 =λ
=λ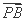 得P点坐标为
得P点坐标为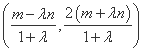 ,
,
将P点坐标代入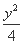 -x2=1,化简得mn=
-x2=1,化简得mn=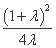 .
.
设∠AOB=2θ,∵tan(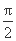 -θ)2.
-θ)2.
∴tan θ=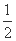 ,sin 2θ=
,sin 2θ=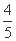 .
.
又|OA|=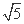 m,|OB|=
m,|OB|=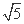 n,
n,
∴S△AOB=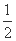 |OA|·|OB|·sin 2θ
|OA|·|OB|·sin 2θ
=2mn
=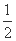
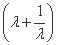 +1,
+1,
记S(λ)= 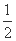
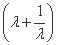 +1,λ∈
+1,λ∈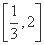 .
.
则S′(λ)= 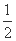
 .
.
由S′(λ)=0得λ=1.
又S(1)=2,S =
=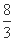 ,S(2)=
,S(2)= 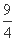 ,
,
∴当λ=1时,△AOB的面积取得最小值2,当λ=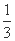 时,
时,
△AOB的面积取得最大值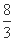 .
.
∴△AOB面积的取值范围是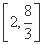 .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
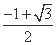 (B)
(B)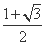
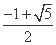 (D)
(D)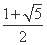
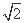 x (B)y=±
x (B)y=± x
x (B)
(B)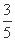 (C)
(C) (D)
(D)
 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )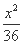 -
- 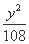 =1 (B)
=1 (B)  -
-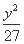 =1
=1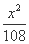 -
-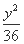 =1 (D)
=1 (D) 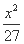 -
-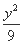 =1
=1