题目内容
6.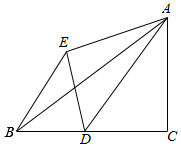 如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.(1)当t为何值时,△BDE是以BE为底的等腰三角形?
(2)当t为何值时,用BD,DE、AD的长度作为线段所围成的三角形是以BD为直角边的直角三角形?
分析 (1)经过时间t,则由题意可得CD=t,DB=8-t,DE=DC.再根据△BDE是以BE为底的等腰三角形,可得DE=DB=DC=4,此时,t=4.
(2)由题意可得CD=t=DE,BD=8-t,AD=$\sqrt{{t}^{2}+36}$,根据题意可得t2+(8-t)2=t2+36,由此求得t的值.
解答 解:(1)经过时间t,CD=t,DB=8-t,∵△ADE和△ADC关于AD成轴对称,∴DE=DC.
根据,BC=8,△BDE是以BE为底的等腰三角形,可得DE=DB=DC=4,此时,t=4.
(2)由题意可得CD=t=DE,BD=8-t,AD=$\sqrt{{t}^{2}+36}$,
根据用BD,DE、AD的长度作为线段所围成的三角形是以BD为直角边的直角三角形,
可得t2+(8-t)2=t2+36,求得t=2,或t=14,
故当t=2,或t=14时,用BD,DE、AD的长度作为线段所围成的三角形是以BD为直角边的直角三角形.
点评 本题主要考查解三角形的实际应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
16.不等式|x+1|-|x-5|<4的解集为( )
| A. | (-∞,4) | B. | (-∞,-4) | C. | (4,+∞) | D. | (-4,+∞) |
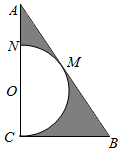 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.