题目内容
16．不等式|x+1|-|x-5|＜4的解集为（ ）| A． | （-∞，4） | B． | （-∞，-4） | C． | （4，+∞） | D． | （-4，+∞） |
分析 通过讨论x的范围，求出各个阶段上的x的范围，取并集即可．
解答 解：x≥5时：
x+1-x+5=6＞4，不等式无解；
-1＜x＜5时：
x+1+x-5＜4，解得：x＜4；
x≤-1时：
-x-1+x-5＜4恒成立．
故不等式的解集是（-∞，4）．
点评 本题考查了绝对值不等式问题，考查分类讨论思想，是一道基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点．
1．为了增强环保意识，某校从男生中随机制取了60人，从女生中随机制取了50人参加环保知识测试，统计数据如表所示，经计算K2=7.822，则环保知识是否优秀与性别有关的把握为（ ）
附：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}{n}_{+2}}$
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P（K2≥k） | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
| A． | 90% | B． | 95% | C． | 99% | D． | 99.9% |
8．等比数列{an}的前n项和为Sn，已知S4=a2+a3+9a1，a5=32，则a1=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | -2 |
5．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}+2x，x≤0\\ ln（x+1），x＞0\end{array}\right.$，若对x∈R都有|f（x）|≥ax，则实数a的取值范围是（ ）
| A． | （-∞，0] | B． | [-2，0] | C． | [-2，1] | D． | （-∞，1] |
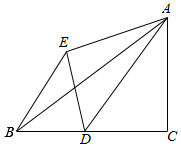如图，△ABC中，∠C=90°，AC=6，BC=8，点D从点C出发，以每秒1个单位的速度沿着CB向点B运功，△ADE和△ADC关于AD成轴对称，连接BE，设点D运动时间为t秒．