题目内容
1.已知椭圆C的中心在坐标原点,长轴在x轴上,离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C上的一点P到椭圆C的两个焦点的距离之和为8.(1)求椭圆C的方程;
(2)求以椭圆C内的点M(1,1)为中点的弦所在的直线方程.
分析 (1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),运用椭圆的定义和离心率公式,解方程可得a,b,进而得到椭圆方程;
(2)设以椭圆C内的点M(1,1)为中点的弦为AB,A(x1,y1)、B(x2,y2),代入椭圆方程,作差,再由中点坐标公式和直线的斜率公式,可得直线AB的斜率,再由点斜式方程可得所求直线的方程.
解答 解:(1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),
则e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,2a=8,解得a=4,c=2$\sqrt{3}$,
则b2=a2-c2=4,
可得椭圆C的方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$;
(2)设以椭圆C内的点M(1,1)为中点的弦为AB,
A(x1,y1)、B(x2,y2),
则x12+4y12=16,①x22+4y22=16,②
x1+x2=2,y1+y2=2,③
①②作差,代入③,可得2(x1-x2)+4×2(y1-y2)=0,
可得${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=-\frac{1}{4}$,
即有直线AB的方程为y-1=-$\frac{1}{4}$(x-1),
即x+4y-5=0.
点评 本题考查椭圆的方程的求法,注意运用椭圆的离心率公式和定义,考查中点弦方程的求法,注意运用点差法和中点坐标公式以及斜率公式,考查化简整理的能力,属于中档题.

练习册系列答案
相关题目
12.已知集合A={-2,-1,0,1,2,3},B={x|x2-2x-3<0},则A∩B=( )
| A. | {-1,0} | B. | {0,1,2} | C. | {-1,0,1} | D. | {-2,-1,0} |
 如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.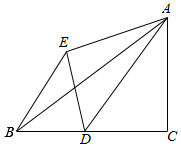 如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.