题目内容
5.已知函数f(x)=aex-x(a∈R),其中e为自然对数的底数,e=2.71828…(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e-x恒成立,求a的取值范围.
分析 (Ⅰ)求出原函数的导函数,然后对a分类,当a≤0时,f′(x)<0,f(x)=aex-x为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性;
(Ⅱ)x∈[1,2],不等式f(x)≥e-x恒成立,等价于aex-x≥e-x恒成立,分离参数a,可得$a≥\frac{1+x{e}^{x}}{{e}^{2x}}$恒成立.令g(x)=$\frac{1+x{e}^{x}}{{e}^{2x}}$,则问题等价于a不小于函数g(x)在[1,2]上的最大值,然后利用导数求得函数g(x)在[1,2]上的最大值得答案.
解答 解:(Ⅰ)由f(x)=aex-x,得f′(x)=aex-1,
当a≤0时,f′(x)<0,f(x)=aex-x为R上的减函数;
当a>0时,令aex-1=0,得x=lna,
若x∈(-∞,-lna),则f′(x)<0,此时f(x)为的单调减函数;
若x∈(-lna,+∞),则f′(x)>0,此时f(x)为的单调增函数.
综上所述,当a≤0时,f(x)=aex-x为R上的减函数;
当a>0时,若x∈(-∞,-lna),f(x)为的单调减函数;
若x∈(-lna,+∞),f(x)为的单调增函数.
(Ⅱ)由题意,x∈[1,2],不等式f(x)≥e-x恒成立,等价于aex-x≥e-x恒成立,
即x∈[1,2],$a≥\frac{1+x{e}^{x}}{{e}^{2x}}$恒成立.
令g(x)=$\frac{1+x{e}^{x}}{{e}^{2x}}$,则问题等价于a不小于函数g(x)在[1,2]上的最大值.
由g(x)=$\frac{1+x{e}^{x}}{{e}^{2x}}$=$\frac{1}{{e}^{2x}}+\frac{x}{{e}^{x}}$,函数y=$\frac{1}{{e}^{2x}}$在[1,2]上单调递减,
令h(x)=$\frac{x}{{e}^{x}}$,x∈[1,2],h′(x)=$\frac{{e}^{x}-x{e}^{x}}{{e}^{2x}}=\frac{1-x}{{e}^{x}}≤0$.
∴h(x)=$\frac{x}{{e}^{x}}$在x∈[1,2]上也是减函数,
∴g(x)在x∈[1,2]上也是减函数,
∴g(x)在[1,2]上的最大值为g(1)=$\frac{1}{{e}^{2}}+\frac{1}{e}$.
故x∈[1,2],不等式f(x)≥e-x恒成立的实数a的取值范围是[$\frac{1}{{e}^{2}}+\frac{1}{e}$,+∞).
点评 本题考查利用导数研究函数的单调性,考查函数最值的求法,训练了利用分离变量法求函数的最值,是中档题.

| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |
| x | 2 | 3 | 4 | 5 |
| y | 6.5 | m | n | 2.5 |
| A. | $\stackrel{∧}{y}$=0.8x+2.3 | B. | $\stackrel{∧}{y}$=2x+0.4 | C. | $\stackrel{∧}{y}$=-1.5x+8 | D. | $\stackrel{∧}{y}$=-1.6x+10 |
| A. | ?x∈R,2x>x2 | B. | ?x∈R,ex<0 | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | ac2>bc2是a>b的充分不必要条件 |
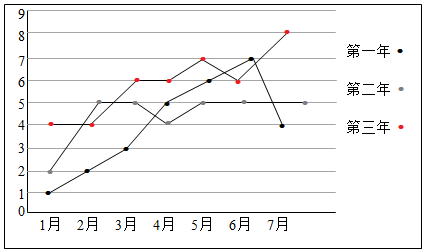
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |