题目内容
函数y=
的单调递增区间为( )
| x2-3x+2 |
A、[
| ||
B、(-∞,
| ||
| C、[2,+∞) | ||
| D、(-∞,1] |
考点:复合函数的单调性
专题:函数的性质及应用
分析:令t(x)=x2-3x+2≥0,求得函数的定义域为(-∞,-1]∪[2,+∞),且函数y=
,本题即求二次函数t(x)在(-∞,-1]∪[2,+∞)上的增区间.再利用二次函数的性质可得t(x)在(-∞,-1]∪[2,+∞)上的增区间.
| t(x) |
解答:
解:令t(x)=x2-3x+2≥0,求得 x≤1,或x≥2,故函数的定义域为(-∞,-1]∪[2,+∞),且函数y=
,
故本题即求二次函数t(x)在(-∞,-1]∪[2,+∞)上的增区间.
再利用二次函数的性质可得t(x)在(-∞,-1]∪[2,+∞)上的增区间为[2,+∞),
故选:C.
| t(x) |
故本题即求二次函数t(x)在(-∞,-1]∪[2,+∞)上的增区间.
再利用二次函数的性质可得t(x)在(-∞,-1]∪[2,+∞)上的增区间为[2,+∞),
故选:C.
点评:本题主要考查二次函数的性质,复合函数的单调性,体现了转化的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=cos2x+2sinx的最大值与最小值的和是( )
| A、-2 | ||
| B、0 | ||
C、-
| ||
D、-
|
设a3=8,求(a-1)(a+1)(a2-a+1)(a2+a+1)的值是( )
| A、7 | B、15 | C、35 | D、63 |
由大于-8小于20的奇数所组成的集合( )
| A、{x∈Z|-8<x<20} |
| B、{x|-8<x<20,x=2k+1,k∈N} |
| C、{x|-8<x<20} |
| D、{x|-8<x<20,x=2k+1,k∈Z} |
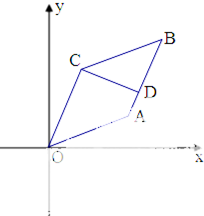 如图,在平行四边形OABC中,已知点A(3,1),C(1,3).
如图,在平行四边形OABC中,已知点A(3,1),C(1,3).