Question

已知正方体ABCD-A₁B₁C₁D₁的棱长为a，E，F分别是棱AB，BC上的点，且AE=BF，若A₁E与C₁F所成的角最小，则有（　　）

• A、AE=BF=

  1

  4

  a
• B、AE=BF=

  1

  3

  a
• C、AE=BF=

  2

  5

  a
• D、AE=BF=

  1

  2

  a

Answer 1

考点：空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：先画出图象，设|AE|=|BF|=x，x∈（0，a），表示出

A1E

，

C1F

，cos＜

A1E

，

C1F

＞=

a2

(x2+a2)[a2+(a-x)2]

，另设分母中；f（x）=（x²+a²）[a²+（a-x）²]，通过求导得出f（x）在x=

1

2

a时，取到最小值，从而得出答案．

解答： 解：如图示：
，
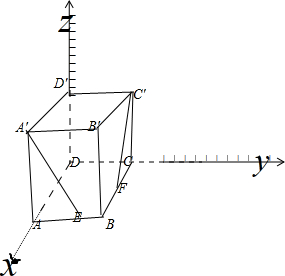设|AE|=|BF|=x，x∈（0，a），∴

A1E

=（0，x-a），

C1F

=（a-x，-a），
∴cos＜

A1E

，

C1F

＞=

A1E • C1F

| A1E |•| C1F |

=

a2

(x2+a2)[a2+(a-x)2]

，
另设分母中；f（x）=（x²+a²）[a²+（a-x）²]，
∴f′（x）=2[（2x³-ax²）-a（2x²-3ax+a²）]
=2（2x-a）（x²-ax+a），
又∵f″（x）=6（2x²-2ax+a²）＞0，
∴f′（x）是增函数，
∴只能有1个零点x=

1

2

a，
∴f（x）在x=

1

2

a时，取到最小值，
∴AE=BF=

1

2

a，
故选：D．

点评：本题考查了用向量表示角的余弦值，考查了函数的最值问题，导数的应用，考查转化思想，是一道中档题．