题目内容
16.据统计,2015年“双11”天猫总成交金额突破912亿元.某购物网站为优化营销策略,对在11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)女性消费情况:
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女士 | 男士 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
附:
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (Ⅰ)根据分层抽样方法求出x、y的值,利用列举法计算基本事件数,求出对应的概率;
(Ⅱ)列出2×2列联表,计算观测值K2,对照表中数据,判断结论是否成立即可.
解答 解:(Ⅰ)依题意,女性应抽取80名,男性应抽取20名 …(1分)
∴x=80-(5+10+15+47)=3…(2分)
y=20-(2+3+10+2)=3…(3分)
抽出的100名且消费金额在[800,1000](单位:元)的网购者中有三位女性设为A,B,C;两位男性设为a,b,从5人中任选2人的基本事件有:(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10件…(4分)
设“选出的两名网购者恰好是一男一女”为事件A
事件A包含的基本事件有:(A,a),(A,b),(B,a),(B,b),(C,a),(C,b)共6件…(5分)
∴p(A)=$\frac{6}{10}$=$\frac{3}{5}$,
(Ⅱ)(Ⅱ)2×2列联表如下表所示
| 女性 | 男性 | 总计 | |
| 网购达人 | 50 | 5 | 55 |
| 非网购达人 | 30 | 15 | 45 |
| 总计 | 80 | 20 | 100 |
∵9.091>6.635且P(k2≥6.635)=0.010…(11分)
答:我们有99%的把握认为“是否为‘网购达人’”与性别有关…(12分)
点评 本题考查了分层抽样方法的应用问题,也考查了2×2列联表的应用问题,属于中档题.

练习册系列答案
相关题目
7.设z=4x•2y中变量x,y满足条件$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$,则z的最小值为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
4.在二项式${({\sqrt{x}+\frac{1}{{2•\root{6}{x}}}})^n}$的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
1.设θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$,则sinθ+$\sqrt{3}$cosθ=( )
| A. | -1 | B. | 1 | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
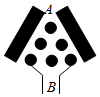 将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.
将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.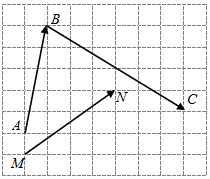 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.