题目内容
4.在二项式${({\sqrt{x}+\frac{1}{{2•\root{6}{x}}}})^n}$的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
分析 利用二项式定理的通项公式、等差数列的性质可得n,再利用通项公式可得有理项与无理项的项数.利用“插空法”及其排列公式即可得出概率.
解答 解:在二项式${({\sqrt{x}+\frac{1}{{2•\root{6}{x}}}})^n}$的展开式中,前三项分别为:$(\sqrt{x})^{n}$,${∁}_{n}^{1}(\sqrt{x})^{n-1}(\frac{1}{2\root{6}{x}})$即$\frac{1}{2}n{x}^{\frac{3n-4}{6}}$,${∁}_{n}^{2}(\sqrt{x})^{n-2}(\frac{1}{2\root{6}{x}})^{2}$即$\frac{n(n-1)}{8}{x}^{\frac{3n-8}{6}}$.
∵前三项的系数成等差数列,
∴$2×\frac{1}{2}n$=1+$\frac{n(n-1)}{8}$,
化为:n2-9n+8=0,
解得n=8.
由通项公式可得:Tr+1=${∁}_{8}^{r}$$(\sqrt{x})^{8-r}$$(\frac{1}{2\root{6}{x}})^{r}$=$(\frac{1}{2})^{r}$${∁}_{8}^{r}$${x}^{4-\frac{2r}{3}}$.
可知当r=0,3,6时,为有理项,其余6项为无理项.
∴有理项都互不相邻的概率p=$\frac{{A}_{7}^{3}{A}_{6}^{6}}{{A}_{9}^{9}}$=$\frac{5}{12}$.
故选:D.
点评 本题考查了二项式定理的应用、等差数列的性质、“插空法”、排列公式、概率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
14.已知函数f(x)=$\frac{1}{3}$x3+ax2+2x+2的图象在点(x0,f(x0))处的切线与直线x+y+1=0垂直,则实数a的取值范围为( )
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
9.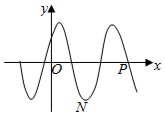 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
16.据统计,2015年“双11”天猫总成交金额突破912亿元.某购物网站为优化营销策略,对在11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性消费情况:
男性消费情况:
(Ⅰ)计算x,y的值;在抽出的100名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(Ⅱ)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
附:
(k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
女性消费情况:
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女士 | 男士 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
附:
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
