题目内容
已知函数
在
处取得极值0，则
= .
11
【解析】
试题分析：由
，得：
因为函数
在
处取得极值0，
所以，
，解得：
或
当时，
所以函数在R上为单调递增函数，与在在处取得极值0相矛盾，所以不合题意，舍去；
当时，
所以，
，且当
时，
，函数
在区间
上为减函数，
当
时，
，函数 在区间
上为增函数，
所以函数在处取得极值.所以符合题意.所以
，所以答案应填：11.
考点：1、导数的几何意义；2、导数在研究函数性质中的应用.
练习册系列答案
步步高达标卷系列答案
相关题目
中，
，
，
.
是等差数列，并求
的通项公式；
的前
项和为
，证明：
.
的参数方程：
（
为参数）和圆
的极坐标方程：
．
的直角坐标方程；
与圆
的位置关系．
，
且
”是“数列
为等比数列”的（ ）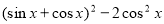
(
)．
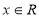在[0，
]上有两个不同的零点x1、x2，求tan(x1＋x2)的值．
，
，若对于任一实数
，
与
至少有一个为正数，则实数
的取值范围是 ( )
是
的充分条件
，
的充要条件是
．
的单调区间；
时，
．