题目内容
(本小题满分14分)已知在数列 中,
中, ,
, ,
, .
.
(1)证明数列 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
(1) ;(2)证明见解析
;(2)证明见解析
【解析】
试题分析:(1)证明一个数列是否为等差数列的基本方法有两种:一是定义法:证明 (
( ,
, 为常数;二是等差中项法,证明
为常数;二是等差中项法,证明 ,若证明一个数列不是等差数列,则只需举出反例即可;(2)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
,若证明一个数列不是等差数列,则只需举出反例即可;(2)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
试题解析:(1)由 ,得
,得 , (2分)
, (2分)
两式相减,得 ,即
,即 , (4分)
, (4分)
所以数列 是等差数列. (5分)
是等差数列. (5分)
由 ,得
,得 ,所以
,所以 , (6分)
, (6分)
故
 . (8分)
. (8分)
(2)因为 ,(11分)
,(11分)
所以

 (
( ) (14分)
) (14分)
考点:1、证明数列是等差数列;2、等差数列的通项公式;3、裂项求数列的和.

练习册系列答案
相关题目
 ﹣
﹣ =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x C.y=±
x C.y=± x D.y=±
x D.y=± x
x 均为单位向量,且
均为单位向量,且 ,则
,则 与
与 夹角为( )
夹角为( )  B.
B. C.
C. D.
D.
 是定义在
是定义在 上的奇函数,则
上的奇函数,则 = .
= .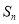 是等差数列
是等差数列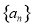 的前
的前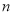 项和,已知
项和,已知 49,则
49,则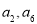 的等差中项是
的等差中项是 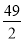 B.7 C.
B.7 C.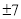 D.
D.
 的方程为
的方程为 ,则点
,则点 到直线
到直线 的距离为 .
的距离为 .
 ,
, ,则
,则 的最小值是 .
的最小值是 .  在
在 处取得极值0,则
处取得极值0,则 = .
= .