题目内容
(本小题满分7分)选修4-4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)判断直线 与圆
与圆 的位置关系.
的位置关系.
(1) ,(2)相交,
,(2)相交,
【解析】
试题分析:先把直线的参数方程中的参数 ,得到直角坐标方程;再把圆的极坐标方程化为直角坐标方程,根据圆心到直线的距离与圆的半径之间的大小关系判断直线与圆的位置关系;
,得到直角坐标方程;再把圆的极坐标方程化为直角坐标方程,根据圆心到直线的距离与圆的半径之间的大小关系判断直线与圆的位置关系;
试题解析:(1)把直线 的参数方程:
的参数方程: (
( 为参数)消去参数
为参数)消去参数 ,得直线
,得直线 的方程为
的方程为 ;
;
再把圆 的极坐标方程:
的极坐标方程: ,即
,即 两边同乘以
两边同乘以 得:
得:

 ,所以
,所以 ,
, 的的直角坐标方程为:
的的直角坐标方程为:
(2)圆心C到直线 的距离
的距离 ,所以直线
,所以直线 与圆C相交.
与圆C相交.
考点:极坐标与参数方程

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 均为单位向量,且
均为单位向量,且 ,则
,则 与
与 夹角为( )
夹角为( )  B.
B. C.
C. D.
D.
 ,
, ,则
,则 的最小值是 .
的最小值是 . 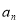 },
},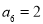 ,则此数列的前11项的和
,则此数列的前11项的和
 ,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
 的值;
的值; ,求
,求 的分布列和数学期望.
的分布列和数学期望.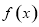 定义域
定义域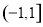 ,满足
,满足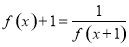 ,当
,当 时,
时,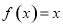 ,若函数
,若函数 ,方程
,方程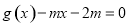 有三个实根,则实数
有三个实根,则实数 的取值范围是( )
的取值范围是( )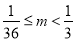 B.
B.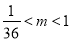 C.
C.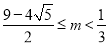 D.
D.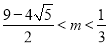
 在
在 处取得极值0,则
处取得极值0,则 = .
= . 中,以直线
中,以直线 为渐近线,且经过抛物线
为渐近线,且经过抛物线 焦点的双曲线的方程是 .
焦点的双曲线的方程是 .