题目内容
(本题满分12分)已知函数f(x)=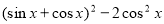 (
(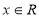 ).
).
(1)求函数f(x)的周期和递增区间;
(2)若函数 在[0,
在[0, ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
(1) 周期为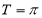 ,[
,[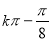 ,
,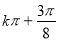 ](
](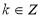 );(2)
);(2) 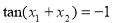 .
.
【解析】
试题分析:(1)利用三角函数的恒等变换将函数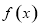 的解析式化成只含一个角一个三角函数的形式,然后再利用正弦函数的性质求出
的解析式化成只含一个角一个三角函数的形式,然后再利用正弦函数的性质求出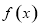 的单调递增区间;
的单调递增区间;
(2)因为函数 的零点可看作是函数
的零点可看作是函数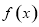 的图象与直线
的图象与直线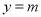 的交点的横坐标,可根据函数
的交点的横坐标,可根据函数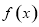 的图象的特征研究
的图象的特征研究 的关系,从而求出
的关系,从而求出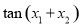 的值.
的值.
试题解析:【解析】
(1)∵f(x)= (
(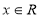 ).
).
由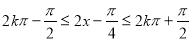
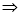
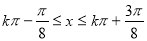 (
(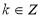 ),
),
∴函数f(x)的周期为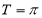 ,递增区间为[
,递增区间为[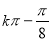 ,
,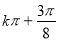 ](
](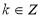 );
);
(2)∵方程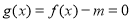 同解于
同解于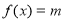 ;
;
在直角坐标系中画出函数f(x)=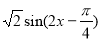 在[0,
在[0,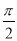 ]上的图象,
]上的图象,
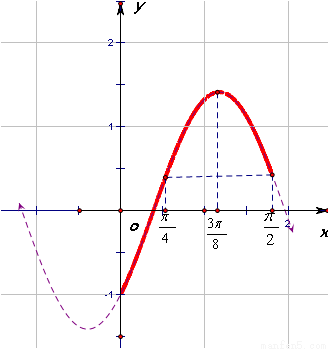
由图象可知,当且仅当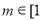 ,
,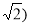 时,方程
时,方程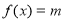 在[0,
在[0,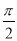 ]上的区间[
]上的区间[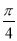 ,
,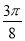 )和(
)和(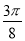 ,
,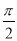 ]有两个不同的解x1、x2,且x1与x2关于直线
]有两个不同的解x1、x2,且x1与x2关于直线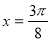 对称,即
对称,即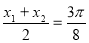 ,∴
,∴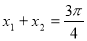 ;故
;故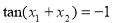 .
.
考点:1、正弦函数的图象与性质;2、三角函数的恒等变换;3、函数与方程的思想以及数形结合的思想.

练习册系列答案
相关题目
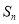 是等差数列
是等差数列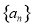 的前
的前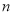 项和,已知
项和,已知 49,则
49,则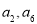 的等差中项是
的等差中项是 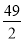 B.7 C.
B.7 C.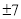 D.
D.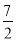
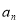 },
},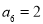 ,则此数列的前11项的和
,则此数列的前11项的和
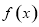 定义域
定义域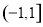 ,满足
,满足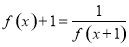 ,当
,当 时,
时,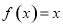 ,若函数
,若函数 ,方程
,方程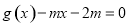 有三个实根,则实数
有三个实根,则实数 的取值范围是( )
的取值范围是( )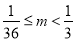 B.
B.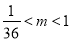 C.
C.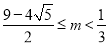 D.
D.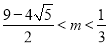

 B.
B. C.
C. D.
D.
 在
在 处取得极值0,则
处取得极值0,则 = .
= .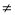 1,函数f(x)=
1,函数f(x)=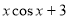 (-1
(-1 1),设函数f(x)的最大值是M,最小值是N,则( )
1),设函数f(x)的最大值是M,最小值是N,则( ) ,则cos(
,则cos( )的值为 .
)的值为 .
 B、
B、 C、
C、 D、
D、