题目内容
若实数x,y满足约束条件
,则z=x+2y的取值范围是( )
|
| A、[0,1] |
| B、[1,6] |
| C、[0,6] |
| D、[2,6] |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的取值范围.
解答:
解:作出不等式对应的平面区域,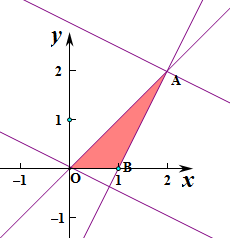
由z=x+2y,得y=-
x+
,
平移直线y=-
x+
,由图象可知当直线y=-
x+
经过点A时,直线y=-
x+
的截距最大,此时z最大.
由
,得
,
即A(2,2),
此时z的最大值为z=2+2×2=6,
当直线y=-
x+
经过点O时,直线y=-
x+
的截距最小,此时z最小.
此时z的最小值为z=0,
故0≤z≤6,
故选:C.

由z=x+2y,得y=-
| 1 |
| 2 |
| z |
| 2 |
平移直线y=-
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
由
|
|
即A(2,2),
此时z的最大值为z=2+2×2=6,
当直线y=-
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
此时z的最小值为z=0,
故0≤z≤6,
故选:C.
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
相关题目
在等差数列{an}中,a1=1,a3=5,则a5=( )
| A、3 | B、5 | C、7 | D、9 |
已知f(3x)=x•log23,则f(2)+f(4)+f(8)+…+f(28)=( )
| A、18 | B、36 | C、72 | D、144 |
| 5 |
| 2-i |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
已知下列三个命题:
①棱长为2的正方体外接球的体积为4
π;
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线x-
y+1=0被圆(x-1)2+y2=4截得的弦长为2
.
其中真命题的序号是( )
①棱长为2的正方体外接球的体积为4
| 3 |
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线x-
| 3 |
| 3 |
其中真命题的序号是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
若a,b,c∈C(C为复数集),则(a-b)2+(b-c)2=0是a=b=c的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
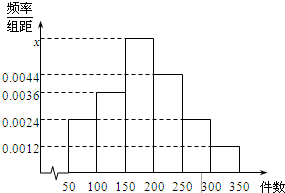 从某工厂抽取50名工人进行调查,发现他们一天加工零件的个数在50至350个之间,现按生产的零件个数将他们分成六组,第一组[50,100),第二组[100,150),第三组[150,200),第四组[200,250),第五组[200,250),第六组[300,350),相应的样本频率分布直方图如图所示:
从某工厂抽取50名工人进行调查,发现他们一天加工零件的个数在50至350个之间,现按生产的零件个数将他们分成六组,第一组[50,100),第二组[100,150),第三组[150,200),第四组[200,250),第五组[200,250),第六组[300,350),相应的样本频率分布直方图如图所示: