题目内容
已知下列三个命题:
①棱长为2的正方体外接球的体积为4
π;
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线x-
y+1=0被圆(x-1)2+y2=4截得的弦长为2
.
其中真命题的序号是( )
①棱长为2的正方体外接球的体积为4
| 3 |
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线x-
| 3 |
| 3 |
其中真命题的序号是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:根据正方体与外接球的关系:正方体的对角线长即为球的直径,再由球的体积公式即可判断①;根据平均数和方差的公式即可判断②;根据直线与圆相交的弦长公式:a=2
,先求出圆心到直线的距离d,应用公式即可判断③.
| r2-d2 |
解答:
解:①设正方体的外接球的半径为r,则2r=2
,r=
,则球的体积为
πr3=
π×3
=4
π,故①正确;
②设一组数据为x1,x2,…,xn,它的平均数为a,方差为b,则另一组数据x1+c,x2+c,…,xn+c(c≠0),运用公式即可得,其平均数为a+c,方差为b,故②错;
③圆(x-1)2+y2=4的圆心为(1,0),半径为2,直线x-
y+1=0到圆的距离为
=1,则直线被圆截得的弦长为2
=2
,故③正确.
故正确的序号为①③.
故选C.
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
②设一组数据为x1,x2,…,xn,它的平均数为a,方差为b,则另一组数据x1+c,x2+c,…,xn+c(c≠0),运用公式即可得,其平均数为a+c,方差为b,故②错;
③圆(x-1)2+y2=4的圆心为(1,0),半径为2,直线x-
| 3 |
| |1-0+1| | ||
|
| 22-1 |
| 3 |
故正确的序号为①③.
故选C.
点评:本题以命题的真假为载体,考查正方体与外接球的关系,平均数与方差的运算,以及直线与圆相交的弦长公式,是一道基础题.

练习册系列答案
相关题目
若角α的终边与单位圆交于第三象限的一点P,其横坐标为-
,则tanα=( )
| ||
| 10 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
 已知函数y=f(x)(x∈R)的图象如图所示,则xf′(x)<0的解集为( )
已知函数y=f(x)(x∈R)的图象如图所示,则xf′(x)<0的解集为( )A、(-∞,
| ||||
B、(-∞,0)∪(
| ||||
C、(-∞,
| ||||
D、(-∞,
|
若实数x,y满足约束条件
,则z=x+2y的取值范围是( )
|
| A、[0,1] |
| B、[1,6] |
| C、[0,6] |
| D、[2,6] |
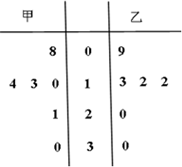 在如图所示的茎叶图中,甲、乙两组数据的平均数分别为
在如图所示的茎叶图中,甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
. |
| S甲 |
. |
| S乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=x+
,则“a=4”是“函数f(x)在(2,+∞)上为增函数”的( )
| a |
| x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |