题目内容
等差数列{am}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d>0,且S3=S8,则S5和S6都是{Sm}中的最小项;
②给定n,对于一切k∈N+(k<n),都有an-k+an+k=2am;
③若d<0,则{Sn}中一定有最大的项;
④存在k∈N+,使ak-ak+1和ak-ak-1同号;
⑤S2013>3(S1342-S671).
其中正确命题的序号为 .
①若d>0,且S3=S8,则S5和S6都是{Sm}中的最小项;
②给定n,对于一切k∈N+(k<n),都有an-k+an+k=2am;
③若d<0,则{Sn}中一定有最大的项;
④存在k∈N+,使ak-ak+1和ak-ak-1同号;
⑤S2013>3(S1342-S671).
其中正确命题的序号为
考点:命题的真假判断与应用
专题:等差数列与等比数列
分析:①由d>0,且S3=S8,利用等差数列的性质易求a6=0,从而可判断①;
②利用等差数列的性质可判断②;
③当d<0时,由Sn=na1+
d=
n2+(a1-
)n,可知{Sn}中一定有最大的项,由此可判断③;
④ak-ak+1和ak-ak-1符号相反,可判断④;
⑤利用S671,S1342-S671,S2013-S1342成等差数列,整理后可判断⑤.
②利用等差数列的性质可判断②;
③当d<0时,由Sn=na1+
| n(n-1) |
| 2 |
| d |
| 2 |
| d |
| 2 |
④ak-ak+1和ak-ak-1符号相反,可判断④;
⑤利用S671,S1342-S671,S2013-S1342成等差数列,整理后可判断⑤.
解答:
解:对于①:∵d>0,且S3=S8,∴a1<0,a4+a5+a6+a7+a8=0,∴5a6=0,即a6=0,
∴S5和S6都是{Sm}中的最小项,故①正确;
对于②:由等差中项的性质可知正确;
对于③:当d<0时,Sn=na1+
d=
n2+(a1-
)n,可知{Sn}中一定有最大的项,故③正确;
对于④:ak-ak+1和ak-ak-1符号相反,故④不正确;
对于⑤:∵S671,S1342-S671,S2013-S1342成等差数列,
∴2(S1342-S671)=S671+(S2013-S1342),
∴S2013=3(S1342-S671),故⑤不正确.
综上所述,正确命题的序号为①②③.
故答案为:①②③.
∴S5和S6都是{Sm}中的最小项,故①正确;
对于②:由等差中项的性质可知正确;
对于③:当d<0时,Sn=na1+
| n(n-1) |
| 2 |
| d |
| 2 |
| d |
| 2 |
对于④:ak-ak+1和ak-ak-1符号相反,故④不正确;
对于⑤:∵S671,S1342-S671,S2013-S1342成等差数列,
∴2(S1342-S671)=S671+(S2013-S1342),
∴S2013=3(S1342-S671),故⑤不正确.
综上所述,正确命题的序号为①②③.
故答案为:①②③.
点评:本题考查等差数列的性质,着重考查等差中项的性质、等差数列前n项和的函数性质及依次n项的和成等差数列等性质的综合应用,属于中档题.

练习册系列答案
相关题目

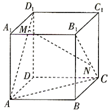 如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是
如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是