题目内容
中心在原点,焦点在x轴上的双曲线的一条渐近线y=
x,且焦距为4过双曲线的左焦点F1作倾斜角为
的弦AB.
(1)求双曲线的标准方程;
(2)求线段AB的长;
(3)设F2为右焦点,求△F2AB的周长.
| 3 |
| π |
| 6 |
(1)求双曲线的标准方程;
(2)求线段AB的长;
(3)设F2为右焦点,求△F2AB的周长.
考点:直线与圆锥曲线的关系,双曲线的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设出双曲线方程,求出渐近线方程,由题意可得,c=2,b=
a,由a,b,c的关系,解除a,b,即可得到双曲线方程;
(2)设出直线AB的方程,代入双曲线方程,解得方程的两根,再由弦长公式,计算即可得到;
(3)求出A,B的坐标,由两点的距离,即可得到△F2AB的周长.
| 3 |
(2)设出直线AB的方程,代入双曲线方程,解得方程的两根,再由弦长公式,计算即可得到;
(3)求出A,B的坐标,由两点的距离,即可得到△F2AB的周长.
解答:
解:(1)设双曲线方程为
-
=1,
则渐近线方程为y=±
x,
由题意可得,c=2,b=
a,
由a2+b2=c2,解得,a=1,b=
,
即有双曲线方程为x2-
=1;
(2)由于F1(-2,0),设直线AB:y=
(x+2),
代入双曲线方程,消去y,得,4x2+4x-5=0,
解得x=
,
由弦长公式得|AB|=
|x1-x2|=
×|
|=2
;
(3)由于F2(2,0),A(
,
),B(
,
),
则△F2AB的周长为|AB|+|AF2|+|BF2|=2
+
+
=2
.
| x2 |
| a2 |
| y2 |
| b2 |
则渐近线方程为y=±
| b |
| a |
由题意可得,c=2,b=
| 3 |
由a2+b2=c2,解得,a=1,b=
| 3 |
即有双曲线方程为x2-
| y2 |
| 3 |
(2)由于F1(-2,0),设直线AB:y=
| ||
| 3 |
代入双曲线方程,消去y,得,4x2+4x-5=0,
解得x=
-1±
| ||
| 2 |
由弦长公式得|AB|=
1+
|
2
| ||
| 3 |
2
| ||
| 2 |
| 2 |
(3)由于F2(2,0),A(
-1-
| ||
| 2 |
| ||||
| 2 |
-1+
| ||
| 2 |
| ||||
| 2 |
则△F2AB的周长为|AB|+|AF2|+|BF2|=2
| 2 |
(
|
(
|
| 6 |
点评:本题考查双曲线的方程和性质,考查直线方程和双曲线方程联立,消去未知数,运用弦长公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
点(x,y)满足的不等式组
(k是常数)所表示的平面区域的边界是一个直角三角形,则x-3y的最小值为( )
|
| A、-3或0 | B、-或0 |
| C、-3 | D、-1 |
若直线与平面所成的角为0°,则该直线与平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
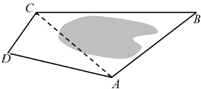 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为