题目内容
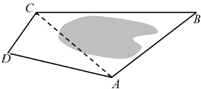如图为了测量A，C两点间的距离，选取同一平面上B，D两点，测出四边形ABCD各边的长度（单位：km）：AB=5，BC=8，CD=3，DA=5，如图所示，且A、B、C、D四点共圆，则AC的长为考点：余弦定理的应用
专题：应用题,解三角形
分析：利用余弦定理，结合∠B+∠D=π，即可求出AC的长．
解答：
解：∵A、B、C、D四点共圆，圆内接四边形的对角和为π．
∴∠B+∠D=π，
∴由余弦定理可得AC2=52+32-2•5•3•cosD=34-30cosD，
AC2=52+82-2•5•8•cosB=89-80cosB，
∵∠B+∠D=π，即cosB=-cosD，
∴-
=
，
∴可解得AC=7．
故答案为：7
∴∠B+∠D=π，
∴由余弦定理可得AC2=52+32-2•5•3•cosD=34-30cosD，
AC2=52+82-2•5•8•cosB=89-80cosB，
∵∠B+∠D=π，即cosB=-cosD，
∴-
| 34-AC2 |
| 30 |
| 89-AC2 |
| 80 |
∴可解得AC=7．
故答案为：7
点评：本题考查余弦定理，考查三角函数知识，正确运用余弦定理是关键，属于基本知识的考查．
练习册系列答案
相关题目
把所有正整数按上小下大，左小右大的原则排成如图所示的数表，其中第i行共有2i-1个正整数．设aij（i、j∈N*）表示位于这个数表中从上往下数第i行，从左往右数第j个数．