题目内容
设f(x)=
sin(2x-
),
(1)解不等式f(x)≥0;
(2)若x∈[0,
],求f(x)的值域.
| 2 |
| π |
| 4 |
(1)解不等式f(x)≥0;
(2)若x∈[0,
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:(1)直接利用正弦函数的单调性,解不等式f(x)≥0,求出解集即可;
(2)通过x∈[0,
],求出相位的范围,利用正弦函数的值域求f(x)的值域.
(2)通过x∈[0,
| π |
| 2 |
解答:
解:(1)∵f(x)≥0,即
sin(2x-
)≥0
∴2kπ≤2x-
≤2kπ+π,k∈Z…(3分)
∴kπ+
≤x≤kπ+
,k∈Z,
∴不等式f(x)≥0的解集为:{x|kπ+
≤x≤kπ+
,k∈Z}…(6分)
(2)∵0≤x≤
,
∴0≤2x≤π,∴-
≤2x-
≤
…(8分)
∴-
≤sin(2x-
)≤1.
∴-1≤
sin(2x-
)≤
∴f(x)的值域为:[-1,
]…(12分).
| 2 |
| π |
| 4 |
∴2kπ≤2x-
| π |
| 4 |
∴kπ+
| π |
| 8 |
| 5π |
| 8 |
∴不等式f(x)≥0的解集为:{x|kπ+
| π |
| 8 |
| 5π |
| 8 |
(2)∵0≤x≤
| π |
| 2 |
∴0≤2x≤π,∴-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
∴-1≤
| 2 |
| π |
| 4 |
| 2 |
∴f(x)的值域为:[-1,
| 2 |
点评:本题考查正弦函数的单调性,正弦函数的最值,考查计算能力以及转化思想.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
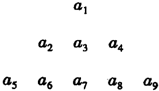 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(45,15) |
| B、M(45,25) |
| C、M(46,16) |
| D、M(46,25) |
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| A、恒取正值或恒取负值 |
| B、有时可以取0 |
| C、恒取正值 |
| D、可以取正值和负值,但不能取0 |
不等式(x2-4)(x-6)2≤0的解集为( )
| A、{x|-2≤x≤2} |
| B、{x|x≥2或x≤-2} |
| C、{x|-2≤x≤2或x=6} |
| D、{x|x≥2} |
若
=(1,2,λ),
=(1,0,0),
=(0,1,0),且
,
,
共面,则λ=( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、1 | B、-1 | C、0 | D、±1 |