题目内容
对某中学高二年级学生是爱好体育还是爱好文娱进行调查,共调查了50人,所得2×2列联表如下:
(1)求出2×2列联表中A、B、C、D、E的值;
(2)若已选出指定的三个男生甲、乙、丙;两个女生M,N,现从中选两人参加某项活动,求选出的两个人恰好是一男一女的概率;
(3)试用独立性检验方法判断性别与爱好体育关系?
参考公式:①K2=
②独立性检验概率表
| 爱好 体育 | 爱好 文娱 | 合计 | |
| 男生 | 15 | A | B |
| 女生 | C | 10 | D |
| 合计 | 20 | E | 50 |
(2)若已选出指定的三个男生甲、乙、丙;两个女生M,N,现从中选两人参加某项活动,求选出的两个人恰好是一男一女的概率;
(3)试用独立性检验方法判断性别与爱好体育关系?
参考公式:①K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
②独立性检验概率表
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
考点:独立性检验的应用
专题:概率与统计
分析:(1)直接利用2×2列联表的定义,求出A、B、C、D、E的值;
(2)直接利用古典概型的求解方法求解即可.
(3)直接利用独立性检验公式求出k2,结合独立性检验概率表说明结果即可.
(2)直接利用古典概型的求解方法求解即可.
(3)直接利用独立性检验公式求出k2,结合独立性检验概率表说明结果即可.
解答:
解:(1)∵C=20-15=5,E=50-20=30,A=30-10=20,B=35,D=15 …(5分)
(2)设选出的两个人恰好是一男一女的事件为A,选出指定的三个男生甲、乙、丙;两个女生M,N,中选两人参加某项活动的基本事件为甲乙、甲丙、甲M、甲N、乙丙、乙M、
乙N、丙M、丙N、MN共10个;…(7分)
事件A有:甲M、甲N、乙M、乙N、丙M、丙N 共6个;…(9分)
求选出的两个人恰好是一男一女的概率P(A)=
…(10分)
(3)假设性别与喜欢体育无关,…(11分)
K2=
=
=
≈0.397<2,706…(13分)
∴没有充分证据显示,认为性别与喜欢体育有关系.…(14分)
(2)设选出的两个人恰好是一男一女的事件为A,选出指定的三个男生甲、乙、丙;两个女生M,N,中选两人参加某项活动的基本事件为甲乙、甲丙、甲M、甲N、乙丙、乙M、
乙N、丙M、丙N、MN共10个;…(7分)
事件A有:甲M、甲N、乙M、乙N、丙M、丙N 共6个;…(9分)
求选出的两个人恰好是一男一女的概率P(A)=
| 3 |
| 5 |
(3)假设性别与喜欢体育无关,…(11分)
K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 50×(15×20-20×5)2 |
| 20×30×35×15 |
| 25 |
| 63 |
∴没有充分证据显示,认为性别与喜欢体育有关系.…(14分)
点评:本题考查独立性检验的应用,2×2列联表的应用,古典概型的计算,基本知识的考查.

练习册系列答案
相关题目
 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
R上可导函数f(x)图象如图所示,则不等式(x2-2x+3)f′(x)>0的解集为( ) 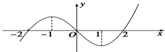

| A、(-∞,-1)∪(1,+∞) |
| B、(-1,1) |
| C、(-∞,-1)∪(-1,0)∪(2,+∞) |
| D、(-∞,-1)∪(-1,1)∪(3,+∞) |
 A.若不等式|2a-1|≤|x+
A.若不等式|2a-1|≤|x+