Question

A．若不等式|2a-1|≤|x+

1

x

|对一切非零实数x恒成立，则实数a的取值范围是

 

．
B．如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段AE的长为

 

．
C．在平面直角坐标系xOy中，已知圆C：

x=5cosθ-1 y=5sinθ+2

（θ为参数）和直线l：

x=4t+6 y=-3t-2

（t为参数），则直线l截圆C所得弦长为

 

．

Answer 1

考点：圆的参数方程,函数恒成立问题,直线的参数方程

专题：坐标系和参数方程

分析：A．利用基本不等式的性质、绝对值不等式的解法即可得出；
B．利用圆的性质、切线的性质、等边三角形的性质、直角三角形的边角关系、平行线的性质、切割线定理即可得出；
C．由圆C：

x=5cosθ-1 y=5sinθ+2

（θ为参数）化为（x+1）²+（y-2）²=25，可得圆心C（-1，2），半径r=5．
直线l：

x=4t+6 y=-3t-2

（t为参数），化为3x+4y-10=0，利用点到直线的距离公式可得圆心C到直线l的距离d，
即可得出直线l截圆C所得弦长=2

r2-d2

．

解答： 解：A．∵|x+

1

x

|≥2，不等式|2a-1|≤|x+

1

x

|对一切非零实数x恒成立，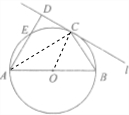
∴|2a-1|≤2，化为-2≤2a-1≤2，解得-

1

2

≤a≤

3

2

，
∴实数a的取值范围是[-

1

2

，

3

2

]，
故答案为：[-

1

2

，

3

2

]．
B．如图所示，连接OC，AC．
则OC⊥l，△OBC为等边三角形．
又AD⊥l，∴OC∥AD．
∴∠DAC=∠ACO=

1

2

∠BOC=30°．
而AC=2OC•cos30°=4

3

．
∴DC=2

3

，AD=2

3

×

3

=6．
∵DC²=DE•DA，
∴DE=

(2 3 )2

6

=2，
∴AE=AD-DE=4．
故答案为：4．   
C．由圆C：

x=5cosθ-1 y=5sinθ+2

（θ为参数）化为（x+1）²+（y-2）²=25，可得圆心C（-1，2），半径r=5．
直线l：

x=4t+6 y=-3t-2

（t为参数），化为3x+4y-10=0，
∴圆心C到直线l的距离d=

|-3+8-10|

5

=1．
∴直线l截圆C所得弦长=2

r2-d2

=2

25-1

=4

6

．
故答案为：4

6

．

点评：本题综合考查了基本不等式的性质、绝对值不等式的解法、圆的性质、切线的性质、等边三角形的性质、直角三角形的边角关系、平行线的性质、切割线定理、圆与直线的参数方程、点到直线的距离公式、弦长=2

r2-d2

，考查了推理能力与计算能力，属于难题．