题目内容
R上可导函数f(x)图象如图所示,则不等式(x2-2x+3)f′(x)>0的解集为( ) 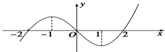

| A、(-∞,-1)∪(1,+∞) |
| B、(-1,1) |
| C、(-∞,-1)∪(-1,0)∪(2,+∞) |
| D、(-∞,-1)∪(-1,1)∪(3,+∞) |
考点:函数的单调性与导数的关系
专题:计算题,函数的性质及应用
分析:由图象可知,在(-∞,-1),(1,+∞)上,f′(x)>0,在(-1,1)上,f′(x)<0;从而求不等式(x2-2x+3)f′(x)>0的解集.
解答:
解:由图可知,
在(-∞,-1),(1,+∞)上,f′(x)>0,
在(-1,1)上,f′(x)<0;
又∵在R上,x2-2x+3>0,
∴不等式(x2-2x+3)f′(x)>0的解集为
(-∞,-1)∪(1,+∞).
故选A.
在(-∞,-1),(1,+∞)上,f′(x)>0,
在(-1,1)上,f′(x)<0;
又∵在R上,x2-2x+3>0,
∴不等式(x2-2x+3)f′(x)>0的解集为
(-∞,-1)∪(1,+∞).
故选A.
点评:本题考查了导数的定义及导数的几何意义,同时考查了不等式的解集的解法,属于基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
(x
-y
)6的展开式中x4y5的系数为( )
| y |
| x |
| A、20 | B、-20 |
| C、-15 | D、15 |
由y=ex、x轴、y轴及直线x=2围成的封闭图形的面积为( )
| A、e2 |
| B、e2-1 |
| C、e2+1 |
| D、e2ln2-1 |
函数y=cos(
x+
)是( )
| 1 |
| 2 |
| π |
| 2 |
| A、周期为2π的偶函数 |
| B、周期为4π的奇函数 |
| C、周期为4π的偶函数 |
| D、周期为π的奇函数 |
已知函数f(x)=
,则不等式f(x)≥2x2-3的解集为( )
|
| A、(0,2] |
| B、[-2,0] |
| C、[-2,2] |
| D、[-2,0)∪(0,2] |