题目内容
已知p:x>1,q:x2-x>0,则¬p是¬q的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的解法求出q,利用充分条件和必要条件的定义进行判断即可.
解答:
解:由x2-x>0得x>1或x<0,即q:x>1或x<0,则¬q:0≤x≤1,
¬p:x≤1,
故¬p是¬q的必要不充分条件,
故答案为:必要不充分
¬p:x≤1,
故¬p是¬q的必要不充分条件,
故答案为:必要不充分
点评:本题主要考查充分条件和必要条件的判断,根据不等式的性质以及复合命题之间的关系是解决本题的关键.

练习册系列答案
相关题目
抛物线x2=2y上的点到直线y=2x-3的最短距离为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
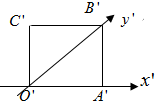 如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )
如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )| A、16cm | ||
| B、8cm | ||
C、(2+3
| ||
D、(2+2
|

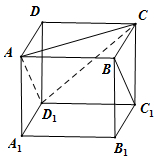 如图,ABCD-A1B1C1D1为正方体,棱长为2.下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,棱长为2.下面结论中正确的结论是