题目内容
12.已知复数z=m(m-1)+(m2+2m-3)i;当实数m取什么值时,复数z是:(1)实数
(2)虚数
(3)纯虚数
(4)零.
分析 对于复数z=a+bi (a,b∈R),(1)当且仅当虚部为0时是实数;(2)虚部不为0时是虚数;(3)当且仅当a=0,b≠0时,复数z是纯虚数;(4)当且仅当a=b=0时,复数z=0.
解答 解:(1)当且仅当m2+2m-3=0,
解得:m=3或m=-1,
即m=3或m=-1时复数是实数;
(2)当且仅当m2+2m-3≠0,
解得:m≠3且m≠-1,
即m≠3且m≠-1时复数是虚数;
(3)当且仅当 $\left\{\begin{array}{l}{m(m-1)=0}\\{{m}^{2}+2m-3≠0}\end{array}\right.$,
解得m=0,
即m=0时,复数z=-3i为纯虚数;
(4)当且仅当 $\left\{\begin{array}{l}{m(m-1)=0}\\{{m}^{2}+2m-3=0}\end{array}\right.$,
解得m=1,
即m=1时,复数z=0.
点评 本题考查了复数的基本概念,深刻理解好基本概念是解决好本题的关键.

练习册系列答案
相关题目
2.某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两人至少有一人参加,那么不同的发言顺序的种数为 ( )
| A. | 360 | B. | 520 | C. | 600 | D. | 720 |
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{4}(x+1)+x-1(x>0)}\\{x-(\frac{1}{4})^{x+1}+3(x≤0)}\end{array}\right.$,若f(x)的两个零点分别为x1,x2,则|x1-x2|=( )
| A. | $\sqrt{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{3}{2}$+ln2 |
7.将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得g(x)的图象,若对满足f(x1)•g(x2)=-1的任意x1,x2,都有|x1-x2|min=$\frac{π}{4}$,则φ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{3}$ |
4. 为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
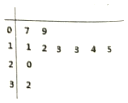
从本市随机抽取了10户家庭,统计了同一个月的用水量,得到如图所示的茎叶图.
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
 为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:| 阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
| 月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
2. 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )| A. | $\frac{π}{2}-\frac{{\sqrt{3}}}{8}$ | B. | $\frac{π}{2}-\frac{{3\sqrt{3}}}{8}$ | C. | $\frac{3π}{2}-\frac{{\sqrt{3}}}{8}$ | D. | $\frac{3π}{2}-\frac{{3\sqrt{3}}}{8}$ |