题目内容
8.如图,某地区有7条南北向街道,5条东西街道,从A点走向B点最短的走法中,必须经过C点的概率( )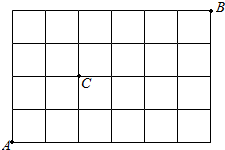
| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
分析 先求出从A到B最短的走法的种数,再求出从A点走向B点最短的走法中,必须经过C点的走法种数,由此能求出从A点走向B点最短的走法中,必须经过C点的概率.
解答 解:10条街道分成6段,每条南北向街道被分成4段,
从A到B最短的走法,无论怎样走,一定包括10段,其中6段方向相同,另4段方向也相同,
每条走法,即是从10段中选出6条,这6段是东西方向的(剩下4段即是走南北方向的),
共有${C}_{10}^{6}$=${C}_{10}^{4}$=210种,
从A点走向B点最短的走法中,必须经过C点,
先从A到C,最短走法有C${\;}_{4}^{2}$=6种,从C到B,最短走法有${C}_{6}^{4}$=15种,
∴从A点走向B点最短的走法中,必须经过C点的概率P=$\frac{{C}_{4}^{2}•{C}_{6}^{4}}{{C}_{10}^{6}}$=$\frac{3}{7}$.
故选:A.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.某企业为了研究员工工作积极性和对待企业改革态度的关系,随机抽取了80名员工进行调查,所得的数据如表所示:
根据上述数据能得出的结论是(参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(b+c)(a+c)(b+d)}$(其中n=a+b+c+d);当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)( )
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 50 | 10 | 60 |
| 工作一般 | 10 | 10 | 20 |
| 合 计 | 60 | 20 | 80 |
| A. | 有99%的把握说事件A与B有关 | B. | 有95%的把握说事件A与B有关 | ||
| C. | 有90%的把握说事件A与B有关 | D. | 事件A与B无关 |
20.下列函数中,在区间(-1,$\frac{π}{2}$)上单调递减的函数为( )
| A. | y=x2 | B. | y=3x-1 | C. | y=log2(x+1) | D. | y=-sinx |