题目内容
19.某企业为了研究员工工作积极性和对待企业改革态度的关系,随机抽取了80名员工进行调查,所得的数据如表所示:| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 50 | 10 | 60 |
| 工作一般 | 10 | 10 | 20 |
| 合 计 | 60 | 20 | 80 |
| A. | 有99%的把握说事件A与B有关 | B. | 有95%的把握说事件A与B有关 | ||
| C. | 有90%的把握说事件A与B有关 | D. | 事件A与B无关 |
分析 先利用公式计算K2,再与临界值比较可得结论
解答 解:K2=80×(50×10-10×10)2÷(60×20×60×20)≈8.88
由于8.88>6.635,
所以有99%的把握说事件A与B有关.
点评 本题考查独立性检验的意义、收集数据的方法,是一个基础题,题目一般给出公式,只要我们代入数据进行运算就可以,注意数字的运算不要出错.

练习册系列答案
相关题目
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[-3,-2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[-3,3]上的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
14.若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则点(a,b)于圆心C之间的最小距离是( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
11. 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
 如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )
如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( )| A. | 86.5,86.7 | B. | 88,86.7 | C. | 88,86.8 | D. | 86,5,86.8 |
8.如图,某地区有7条南北向街道,5条东西街道,从A点走向B点最短的走法中,必须经过C点的概率( )
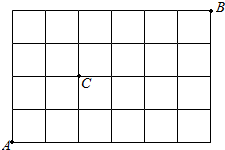

| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
9.若函数f(x)满足f(x)=x2lnx+3xf′(1)-1,则f′(1)等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | 1 |
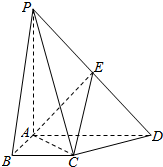 四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.
四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.