题目内容
11.已知函数y=f(x)是R上的偶函数,且在区间(-∞,0)是单调递增的,若S1=$\underset{\stackrel{2}{∫}}{1}$x2dx,S2=$\underset{\stackrel{2}{∫}}{1}$$\frac{1}{x}$dx,S3=$\underset{\stackrel{2}{∫}}{1}$exdx,则f(S1),f(S2),f(S3)的大小关系是f(S3)<f(S1)<f(S2).分析 根据积分的应用,先求出则S3>S1>S2,然后根据函数奇偶性和单调性的关系,判断函数在(0,+∞)上的单调性即可得到结论.
解答 解:S1=$\underset{\stackrel{2}{∫}}{1}$x2dx=$\frac{1}{3}$x3|${\;}_{1}^{2}$=$\frac{8}{3}-\frac{1}{3}$=$\frac{7}{3}$,S2=$\underset{\stackrel{2}{∫}}{1}$$\frac{1}{x}$dx=lnx|${\;}_{1}^{2}$=ln2,S3=$\underset{\stackrel{2}{∫}}{1}$exdx=ex|${\;}_{1}^{2}$=e2-e,
则S3>S1>S2,
∵函数y=f(x)是R上的偶函数,且在区间(-∞,0)是单调递增的,
∴f(x)在区间(-∞,0)是单调递减的,
∴f(S3)<f(S1)<f(S2),
故答案为:f(S3)<f(S1)<f(S2),
点评 本题主要考查函数值的大小比较,根据积分的性质判断S3>S1>S2,然后根据函数奇偶性和单调性的关系进行判断即可.

练习册系列答案
相关题目
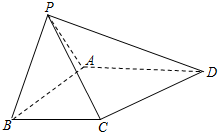 如图,在四棱锥P-ABCD中,锐角三角形PAB所在的平面与底面ABCD垂直,∠PBC=∠BAD=90°.
如图,在四棱锥P-ABCD中,锐角三角形PAB所在的平面与底面ABCD垂直,∠PBC=∠BAD=90°.