题目内容
3．某小区的6个停车位置，有3辆汽车需要停放，若要使三个空位连在一起，则停放的方法数为24（用数字作答）．分析 先放置需要停放的3辆汽车有${A}_{3}^{3}$=6种方法，再将三个连在一起的空位看做一个整体插进已停放的三辆车中间或两边有${C}_{4}^{1}$=4种插法，进而利用分步乘法计数原理计算即得结论．
解答 解：∵需要停放的3辆汽车是不一样的，
∴放置它们的方法有${A}_{3}^{3}$=6种，
然后将三个连在一起的空位看做一个整体，插进已停放的三辆车中间，
由于可以放在两边，故有${C}_{4}^{1}$=4种插法，
所以总数是6×4=24种，
故答案为：24．
点评 本题考查计数原理的应用，考查相邻问题用捆绑法，注意解题方法的积累，属于中档题．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
13．
为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100 分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：
（1）求出频率分布表中①、②、③、④、⑤的值；
（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生获奖？
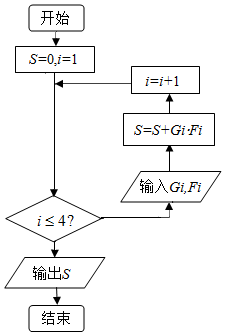
（3）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序的功能是什么？求输出的S的值．
为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100 分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：（1）求出频率分布表中①、②、③、④、⑤的值；
（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生获奖？
（3）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序的功能是什么？求输出的S的值．
| 序号 （i） | 分组 （分数） | 组中值 （Gi） | 频数 （人数） | 频率 （Fi） |
| 1 | [60，70） | 65 | ① | 0.10 |
| 2 | [70，80） | 75 | 20 | ② |
| 3 | [80，90） | 85 | ③ | 0.20 |
| 4 | [90，100） | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
14．“?x＞0，使a+x＜b”是“a＜b”成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
15．动点P（x，y）到点O（0，0）的距离是到点A（3，-3）的距离的$\sqrt{2}$倍，则点P的轨迹方程是（ ）
| A． | x2-12y+y2+12y+36=0 | B． | x2+6x+y2-12y+36=0 | ||
| C． | x2+12x+y2-12y+36=0 | D． | x2-6x+y2+6y+18=0 |