题目内容
2.已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=$\frac{1}{3}f(\frac{1}{3})$,b=-3f(-3),c=$(ln\frac{1}{3})$$f(ln\frac{1}{3})$,则a,b,c的大小关系正确的是( )| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<a<b |
分析 根据式子得出F(x)=xf(x)为R上的偶函数,利用f′(x)+$\frac{f(x)}{x}$>0.当x>0时,x•f′(x)+f(x)>0;当x<0时,x•f′(x)+f(x)<0,判断单调性即可证明a,b,c 的大小.
解答 解:定义域为R的奇函数y=f(x),
设F(x)=xf(x),
∴F(x)为R上的偶函数,
∴F′(x)=f(x)+xf′(x)
∵当x≠0时,f′(x)+$\frac{f(x)}{x}$>0.
∴当x>0时,x•f′(x)+f(x)>0,
当x<0时,x•f′(x)+f(x)<0,
即F(x)在(0,+∞)单调递增,在(-∞,0)单调递减.
F($\frac{1}{3}$)=a=$\frac{1}{3}$f($\frac{1}{3}$)=F(ln$\root{3}{e}$),F(-3)=b=-3f(-3)=F(3),F(ln$\frac{1}{3}$)=c=(ln$\frac{1}{3}$)f(ln$\frac{1}{3}$)=F(ln3),
∵ln$\root{3}{e}$<ln3<3,
∴F(ln$\root{3}{e}$)<F(ln3)<F(3).
即a<c<b,
故选:B.
点评 本题考查了导数在函数单调性的运用,根据给出的式子,得出需要的函数,运用导数判断即可,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.设函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),x<1}\\{{2}^{x},x≥1}\end{array}\right.$,则f(-6)-f(log23)=( )
| A. | 1 | B. | 7 | C. | -1 | D. | 2 |
13. 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
(1)求出频率分布表中①、②、③、④、⑤的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生获奖?
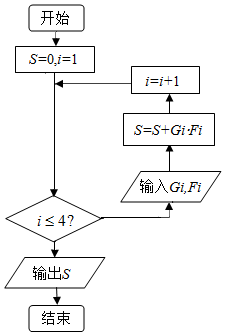
(3)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序的功能是什么?求输出的S的值.
 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:(1)求出频率分布表中①、②、③、④、⑤的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生获奖?
(3)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序的功能是什么?求输出的S的值.
| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
14.“?x>0,使a+x<b”是“a<b”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |