题目内容
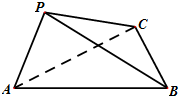 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.(Ⅰ)求直线PC与平面ABC所成角的正弦值;
(Ⅱ)求二面角B-AP-C的余弦值.
考点:二面角的平面角及求法,直线与平面所成的角
专题:空间角
分析:(Ⅰ)过P作PO⊥平面ABC,交AD于O,连接OC,由已知,∠OCP为直线PC与平面ABC所成的角,由此能求出直线PC与平面ABC所成角的正弦值.
(Ⅱ)以O为原点,建立空间直角坐标系,分别求出平面APC的一个法向量和平面ABP的一个法向量,由此利用向量法能求出二面角B-AP-C的余弦值.
(Ⅱ)以O为原点,建立空间直角坐标系,分别求出平面APC的一个法向量和平面ABP的一个法向量,由此利用向量法能求出二面角B-AP-C的余弦值.
解答:
解:(Ⅰ)过P作PO⊥平面ABC,交AD于O,连接OC,
由已知,∠OCP为直线PC与平面ABC所成的角,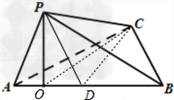
设AB中点为D,连接PD,CD
因为AB=BC=CA,
所以CD⊥AB,
因为∠APB=90°,∠PAB=60°,
所以△PAD为等边三角形,不妨设PA=2,
则OD=1,OP=
,AB=4
所以CD=2
,OC=
=
=
,
PC=
=
=4,
在Rt△OCP中,sin∠OCP=
=
.
故直线PC与平面ABC所成角的正弦值为
.
(Ⅱ)由(Ⅰ)知,以O为原点,建立空间直角坐标系.
则
=(1,0,
),
=(2,2
,0),
设平面APC的一个法向量为
=(x,y,z),
则由
,
取x=-
,则y=1,z=1,所以
=(-
,1,1)
设二面角B-AP-C的平面角为β,由题意知β为锐角
而面ABP的一个法向量为
=(0,1,0),
则cosβ=|
=|
|=
故二面角B-AP-C的余弦值为
.
由已知,∠OCP为直线PC与平面ABC所成的角,

设AB中点为D,连接PD,CD
因为AB=BC=CA,
所以CD⊥AB,
因为∠APB=90°,∠PAB=60°,
所以△PAD为等边三角形,不妨设PA=2,
则OD=1,OP=
| 3 |
所以CD=2
| 3 |
| OD2+CD2 |
| 1+12 |
| 13 |

PC=
| OC2+OP2 |
| 13+3 |
在Rt△OCP中,sin∠OCP=
| OP |
| PC |
| ||
| 4 |
故直线PC与平面ABC所成角的正弦值为
| ||
| 4 |
(Ⅱ)由(Ⅰ)知,以O为原点,建立空间直角坐标系.
则
| AP |
| 3 |
| AC |
| 3 |
设平面APC的一个法向量为
| n |
则由
|
取x=-
| 3 |
| n |
| 3 |
设二面角B-AP-C的平面角为β,由题意知β为锐角
而面ABP的一个法向量为
| m |
则cosβ=|
| ||||
|
|
| 1 | ||
|
| ||
| 5 |
故二面角B-AP-C的余弦值为
| ||
| 5 |
点评:本题考查直线与平面所成角的正弦值的求法,考查二面角的余弦值的求法,涉及到线线、线面、面面平行、垂直的性质及应用,解题时要注意向量法的合理运用,是中档题.

练习册系列答案
相关题目
若sinθ•cosθ=
,则下列结论中一定成立的是( )
| 1 |
| 2 |
A、sinθ=
| ||||
B、sinθ=-
| ||||
| C、sinθ+cosθ=1 | ||||
| D、sinθ-cosθ=0 |
若集合M={x|x<3},N={x|log2x>1},则M∩N=( )
| A、R |
| B、{x|0<x<3} |
| C、{x|1<x<3} |
| D、{x|2<x<3} |
已知sinα+cosα=
,α∈(0,π),则sin2α=( )
| 1 |
| 5 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|