题目内容
已知集合A={x|kπ+
≤x<kπ+π,k∈Z},B={y|y=-x2-2x+4.x∈R},C={y|y=2x-4},则A∩B∩C 用区间表示)
| π |
| 3 |
考点:交集及其运算
专题:函数的性质及应用,集合
分析:先利用函数的性质求解函数的值域得集合B,C,然后求B∩C,令k取不同值(要求包含B∩C)再求A∩B∩C.
解答:
解:∵y=-x2-2x+4=-(x+1)2+5≤5,
∴B={y|y≤5},
又∵y=2x-4>-4,
∴C={y|y>-4},
∴B∩C=(-4,5],
令k=-1,0,1时,A=[-
π,0)∪[
,π)∪[
π,2π),
A∩B∩C=[-
π,0)∪[
,π)∪[
π,5).
故答案为:=[-
π,0)∪[
,π)∪[
π,5).
∴B={y|y≤5},
又∵y=2x-4>-4,
∴C={y|y>-4},
∴B∩C=(-4,5],
令k=-1,0,1时,A=[-
| 2 |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
A∩B∩C=[-
| 2 |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
故答案为:=[-
| 2 |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
点评:本题考察函数的交集运算和利用函数的性质求函数的值域,属于基础题目.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、8 |
命题“?x>0,x2-x≤0”的否定是( )
| A、?x0>0,x02-x0≤0 |
| B、?x0>0,x02-x0>0 |
| C、?x>0,x2-x>0 |
| D、?x≤0,x2-x>0 |
已知角α的终边过点P(-3cosθ,4cosθ),其中θ∈(
,π),则cosα的值是( )
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
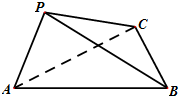 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.