题目内容
已知函数f(x)=
(a是常数且a>0).给出下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③函数f(x)在(-∞,0)上的零点是x=lg
;
④若f(x)>0在[
,+∞)上恒成立,则a的取值范围是[1,+∞);
⑤对任意的x1,x2<0且x1≠x2,恒有f(
)<
.
其中正确命题的序号是 .(写出所有正确命题的序号)
|
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③函数f(x)在(-∞,0)上的零点是x=lg
| 1 |
| 2 |
④若f(x)>0在[
| 1 |
| 2 |
⑤对任意的x1,x2<0且x1≠x2,恒有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:画出函数f(x)=
(a是常数且a>0)的图象,
①由图只需说明在点x=0处函数f(x)的最小值是-1;
②只需说明函数f(x)在R上的单调性即可;
③函数f(x)在(-∞,0)的零点是lg
;
④只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,
从而求得a的取值范围是a>1;
⑤已知函数f(x)的图象在(-∞,0))上是下凹的,所以任取两点连线应在图象的上方.
|
①由图只需说明在点x=0处函数f(x)的最小值是-1;
②只需说明函数f(x)在R上的单调性即可;
③函数f(x)在(-∞,0)的零点是lg
| 1 |
| 2 |
④只需说明f(x)>0在[
| 1 |
| 2 |
| 1 |
| 2 |
从而求得a的取值范围是a>1;
⑤已知函数f(x)的图象在(-∞,0))上是下凹的,所以任取两点连线应在图象的上方.
解答:
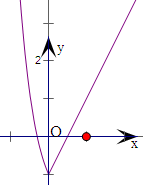 解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
对于②,由图象说明函函数f(x)在R上不是单调函数;故错;
对于③,函数f(x)在(-∞,0)的零点是lg
,故正确;
对于④,只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,求得a的取值范围是a>1;故错;
对于⑤,已知函数f(x)在(-∞,0)上的图象是下凹的,所以任取两点连线应在图象的上方,即f(
)<
,故正确.
故答案为:①③⑤.
 解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
解:对于①,由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;对于②,由图象说明函函数f(x)在R上不是单调函数;故错;
对于③,函数f(x)在(-∞,0)的零点是lg
| 1 |
| 2 |
对于④,只需说明f(x)>0在[
| 1 |
| 2 |
| 1 |
| 2 |
对于⑤,已知函数f(x)在(-∞,0)上的图象是下凹的,所以任取两点连线应在图象的上方,即f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故答案为:①③⑤.
点评:利用函数的图象研究函数的单调区间,以及根据函数的增减性得到函数的最值是常用的方法,解答本题的关键是图象法.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
命题“?x>0,x2-x≤0”的否定是( )
| A、?x0>0,x02-x0≤0 |
| B、?x0>0,x02-x0>0 |
| C、?x>0,x2-x>0 |
| D、?x≤0,x2-x>0 |
设变量x、y满足
,则目标函数z=2x+3y的最小值为( )
|
| A、7 | B、8 | C、22 | D、23 |
函数f(x)=lg(x-1)的定义域为( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
已知函数y=f(x)(x∈R)满足f(x+1)=
,且当x∈[-1,1]时,f(x)=|x|,函数g(x)=
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| 1 |
| f(x) |
|
| A、8 | B、9 | C、10 | D、11 |
已知等比数列{an},且a4+a8=
dx,则a6(a2+2a6+a10)的值为( )
| ∫ | 2 0 |
| 4-x2 |
| A、π2 | B、4 |
| C、π | D、-9π |
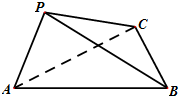 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.