题目内容
已知sinα+cosα=
,α∈(0,π),则sin2α=( )
| 1 |
| 5 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:二倍角的正弦
专题:计算题,三角函数的求值
分析:运用平方法,结合条件的平方关系和二倍角的正弦公式,计算即可得到.
解答:
解:∵sinα+cosα=
,α∈(0,π),
∴(sinα+cosα)2=
,
即sin2α+cos2α+2sinαcosα=
,
即有1+sin2α=
,
即sin2α=-
.
故选A.
| 1 |
| 5 |
∴(sinα+cosα)2=
| 1 |
| 25 |
即sin2α+cos2α+2sinαcosα=
| 1 |
| 25 |
即有1+sin2α=
| 1 |
| 25 |
即sin2α=-
| 24 |
| 25 |
故选A.
点评:本题考查平方法的运用,考查二倍角的正弦公式和同角的平方关系的运用,考查运算能力,属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、8 |
设变量x、y满足
,则目标函数z=2x+3y的最小值为( )
|
| A、7 | B、8 | C、22 | D、23 |
函数f(x)=lg(x-1)的定义域为( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
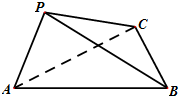 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.