题目内容
已知f(log2x)=
(a∈R,x>0)
(1)求函数y=f(x)的解析式;
(2)判断并用单调性定义证明函数y=f(x)的单调性.
| ax+b | ||
x+
|
(1)求函数y=f(x)的解析式;
(2)判断并用单调性定义证明函数y=f(x)的单调性.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:综合题,函数的性质及应用
分析:(1)利用换元法,令log2x=t,则x=2t,f(t)=
,以x代t,得y=f(x)=
,x∈R.
(2)利用定义,按照取值,作差,比较f(x1)与f(x2)大小关系,做出解答.
| a2t+b | ||
2t+
|
| a2x+b | ||
2x+
|
(2)利用定义,按照取值,作差,比较f(x1)与f(x2)大小关系,做出解答.
解答:
解:(1)∵f(log2x)=
,令log2x=t,则x=2t,∵x>0,∴t∈R,
∴f(t)=
,
以x代t,得y=f(x)=
,x∈R.
(2)设x1,x2,是R上的任意两个实数,且x1<x2,
则f(x1)-f(x2)=
,∵x1<x2,∴2x1-2x2<0,
当b>
a时,f(x1)-f(x2)>0,f(x1)>f(x2),函数y=f(x)在R上是减函数,
当b=
a时,f(x1)-f(x2)=0,f(x1)=f(x2),函数y=f(x)在R上是常函数,
当b<
a时,f(x1)-f(x2)<0,f(x1)<f(x2),函数y=f(x)在R上是增函数.
| ax+b | ||
x+
|
∴f(t)=
| a2t+b | ||
2t+
|
以x代t,得y=f(x)=
| a2x+b | ||
2x+
|
(2)设x1,x2,是R上的任意两个实数,且x1<x2,
则f(x1)-f(x2)=
(
| ||||
(2x1+
|
当b>
| 2 |
当b=
| 2 |
当b<
| 2 |
点评:本题考查函数的概念以及解析式表示函数,考查函数单调性的判断与证明,考查换元法,分类讨论的思想方法.

练习册系列答案
相关题目
已知函数y=f(x)(x∈R)满足f(x+1)=
,且当x∈[-1,1]时,f(x)=|x|,函数g(x)=
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| 1 |
| f(x) |
|
| A、8 | B、9 | C、10 | D、11 |
在△OAB中,|
|=a,|
|=b,OD是AB边上的高,若
=λ
,则实数λ等于( )
| OA |
| OB |
| AD |
| AB |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知等比数列{an},且a4+a8=
dx,则a6(a2+2a6+a10)的值为( )
| ∫ | 2 0 |
| 4-x2 |
| A、π2 | B、4 |
| C、π | D、-9π |
直线y=ax+b(a+b=0)的图象可能是( )
A、 |
B、 |
C、 |
D、 |
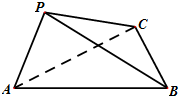 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC.