题目内容
已知函数f(x)=2x,x∈R,若f(2-a2)>f(a),则实数a的取值范围是( )
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:根据函数f(x)=2x在R上是增函数,故由f(2-a2)>f(a),可得 2-a2>a,由此求得实数a的取值范围.
解答:
解:由于函数f(x)=2x在R上是增函数,故由f(2-a2)>f(a),可得 2-a2>a,
求得-2<a<1,
故选:C.
求得-2<a<1,
故选:C.
点评:本题主要考查一元二次不等式的解法,指数函数函数的单调性和特殊点,体现了转化的数学思想,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
国家征收个人所得税是分段计算的,总收入不超过3500的免征个人所得税,超过3500元的部分为全月应纳税额,税率表为:
某人某月总收入为6000元,则他当月应缴纳的税额为( )
| 全月应纳税额 | 税率 |
| 不超过1500元的部分 | 3% |
| 超过1500元至4500元的部分 | 10% |
| 超过4500元至9000元的部分 | 20% |
| A、1200元 | B、2500 |
| C、145元 | D、100元 |
函数y=logax (0<a<1)的图象大致是( )
A、 |
B、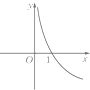 |
C、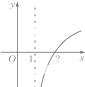 |
D、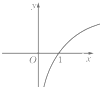 |
下列函数在区间(-∞,0)上为增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-x2-2x-1 | ||
| D、y=1+x2 |
“方程
+
=1表示焦点在y轴上的椭圆”是“n>m>0”的( )
| x2 |
| m2 |
| y2 |
| n2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
f(x)是定义在(-1,1)上的奇函数且单调递减,若f(2-a)+f(4-a2)<0,则a的取值范围是( )
A、(
| ||
B、(-∞,
| ||
C、(
| ||
D、(-∞,
|
已知等比数列{an}中,
=2,a4=8,则a6=( )
| a2+a3 |
| a1+a2 |
| A、31 | B、32 | C、63 | D、64 |
设A,B,C为全集R的子集,定义A-B=A∩(∁RB)( )
| A、若A∩B⊆A∩C,则B⊆C |
| B、若A∩B⊆A∩C,则A∩(B-C)=∅ |
| C、若A-B⊆A-C,则B?C |
| D、若A-B⊆A-C,则A∩(B-C)=∅ |