题目内容
设f(x)是定义在R上奇函数,且当x>0时,f(x)=2x-3,求函数f(x)的解析式.
考点:函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:由函数的奇偶性在对称区间上求解析式,再对称即可.
解答:
解:当x<0时,-x>0,
f(-x)=2-x-3,
又∵f(x)是定义在R上奇函数,
∴f(-x)=-f(x),
∴-f(x)=2-x-3,
∴f(x)=-2-x+3=-
+3,
∴f(x)=
.
f(-x)=2-x-3,
又∵f(x)是定义在R上奇函数,
∴f(-x)=-f(x),
∴-f(x)=2-x-3,
∴f(x)=-2-x+3=-
| 1 |
| 2x |
∴f(x)=
|
点评:本题考查了函数解析式的求法,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知a,b,c满足c<b<a且ac<0,则下列选项中不一定能成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数:①y=xsinx,②y=xcosx,③y=x|cosx|,④y=x2x的图象(部分)如图(但顺序被打乱):则从左到右的各图象依次对应的函数序号是( )
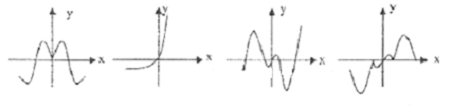

| A、①④②③ | B、①④③② |
| C、④①②③ | D、③④②① |