题目内容
20.已知直线m,n,l,平面α,β.给出下面四个命题:( )①$\left.\begin{array}{l}m⊥α\\ α⊥β\end{array}\right\}⇒m∥β$;
②$\left.\begin{array}{l}m⊥l\\ n⊥l\end{array}\right\}⇒m∥n$;
③$\left.\begin{array}{l}α∥β\\ n?α\end{array}\right\}⇒n∥β$;
④$\left.\begin{array}{l}m∥α\\ m∥n\end{array}\right\}⇒n∥α$.
其中正确是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 在①中,m∥β或m?β;在②中,m与n相交、平行或异面;在③中,由线面平行的判定定理知n∥β;在④中,n∥α或n?α.
解答 解:由直线m,n,l,平面α,β,知:
在①中,$\left.\begin{array}{l}m⊥α\\ α⊥β\end{array}\right\}⇒$m∥β或m?β,故①错误;
在②中,$\left.\begin{array}{l}m⊥l\\ n⊥l\end{array}\right\}⇒$m与n相交、平行或异面,故②错误;
在③中,$\left.\begin{array}{l}α∥β\\ n?α\end{array}\right\}⇒n∥β$,由线面平行的判定定理知n∥β,故③正确;
在④中,$\left.\begin{array}{l}m∥α\\ m∥n\end{array}\right\}⇒$n∥α或n?α,故④错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
20.已知离散型随机变量X的分布列如表所示,则D(X)=( )
| X | -1 | 0 | 1 |
P | $\frac{1}{2}$ | $1-\frac{3}{2}q$ | q2 |
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{17}{16}$ | D. | $\frac{11}{16}$ |
1.如图,四边形ABCD是圆柱的轴截面,E是底面圆周上异于A、B的一点,则下面结论中错误的是( )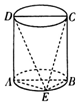

| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
8.若对于定义在R上的函数f(x)当且仅当存在有限个非零自变量x,使得f(-x)=f(x),则称f(x)为类偶函数,若函数f(x)=x3+(a2-2a)x+a为类偶函数,则f(a)的取值范围为( )
| A. | (0,2) | B. | (-∞,0]∪[2,+∞) | C. | [0,2] | D. | (-∞,0]∪(2,+∞) |
15.“双曲线方程为x2-y2=3”是“双曲线离心率e=$\sqrt{2}$”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
9.复数z=$\frac{2-i}{1+2i}$,则$\overline{z}$=( )
| A. | i | B. | 1+i | C. | -i | D. | 1-i |
10.sin$\frac{5π}{3}$的值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
