题目内容
已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx-x,设a=f(-
),b=f(3),c=f(0),则a、b、c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<a<b |
| C、b<c<a |
| D、a<b<c |
考点:函数单调性的性质,函数奇偶性的性质,不等式比较大小
专题:函数的性质及应用
分析:易得函数f(x)的图象关于直线x=1对称,且当x∈(1,+∞)时,函数f(x)=sinx-x单调递减,由对称性可得a=f(
),c=f(2),由单调性可得答案.
| 5 |
| 2 |
解答:
解:∵函数f(x+1)是偶函数,
∴函数f(x)的图象关于直线x=1对称,
又∵当x∈(1,+∞)时,函数f(x)=sinx-x,
∴b=f(3),a=f(-
)=f(
),c=f(0)=f(2),
又x∈(1,+∞)时,f′(x)=cosx-1≤0,
∴当x∈(1,+∞)时,函数f(x)=sinx-x单调递减,
∴b<a<c
故选:A
∴函数f(x)的图象关于直线x=1对称,
又∵当x∈(1,+∞)时,函数f(x)=sinx-x,
∴b=f(3),a=f(-
| 1 |
| 2 |
| 5 |
| 2 |
又x∈(1,+∞)时,f′(x)=cosx-1≤0,
∴当x∈(1,+∞)时,函数f(x)=sinx-x单调递减,
∴b<a<c
故选:A
点评:本题考查函数的单调性和对称性,涉及导数法判函数的单调性,属基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(
| ||
| D、(2,+∞) |
函数y=lg(x2-2x+a)的值域不可能是( )
| A、(-∞,0] | B、[0,+∞) |
| C、[1,+∞) | D、R |
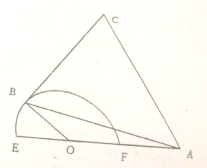 如图,AO=2,B是半个单位圆上的动点,△ABC是等边三角形,求当∠AOB等于多少时,四边形OACB的面积最大,并求四边形面积的最大值.
如图,AO=2,B是半个单位圆上的动点,△ABC是等边三角形,求当∠AOB等于多少时,四边形OACB的面积最大,并求四边形面积的最大值. 已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,通过如图所示算法框图给出的一个算法输出一个整数a,则输出的数a=5的概率是
已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,通过如图所示算法框图给出的一个算法输出一个整数a,则输出的数a=5的概率是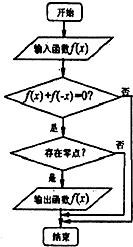 某程序框图如图所示,现依次输入如下四个函数:
某程序框图如图所示,现依次输入如下四个函数: