题目内容
在数列{an}中,a3=1,Sn是其前n项和,且Sn=an+1(n∈N*).
(Ⅰ)求an,Sn;
(Ⅱ)设bn=log2Sn,数列{cn}满足cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,数列{cn}的前n项和为Tn,当n>1时,求使
Tn<2n+
成立的最小正整数n的值.
(Ⅰ)求an,Sn;
(Ⅱ)设bn=log2Sn,数列{cn}满足cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,数列{cn}的前n项和为Tn,当n>1时,求使
| 2 |
| n-1 |
| n+1 |
| 5 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)当n=1时,a1=a2,当n=2时,a1+a2=a3=1,从而a1=a2=
,由
,得2an=an+1,n≥2,从而数列{an}从第二项起是首项为
,公比为2的等比数列,由此能求出an,Sn.
(Ⅱ)由Sn=2n-2,得bn=log2Sn=n-2,从而由cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,得到cn=
+n•2n-2,由此利用分组求和法和裂项求和法求出Tn=
+(n-1)•2n-1,由此能求出当n>1时,使
Tn<2n+
成立的最小正整数n的值为n=4.
| 1 |
| 2 |
|
| 1 |
| 2 |
(Ⅱ)由Sn=2n-2,得bn=log2Sn=n-2,从而由cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,得到cn=
| 1 |
| (n+1)(n+2) |
| n+1 |
| n+2 |
| 2 |
| n-1 |
| n+1 |
| 5 |
解答:
解:(Ⅰ)当n=1时,a1=a2,
当n=2时,a1+a2=a3=1,
∴a1=a2=
,
由
,得an=an+1-an,即2an=an+1,n≥2,
=2,n≥2,∵
=1,
∴数列{an}从第二项起是首项为
,公比为2的等比数列,
∴an=
,
∴Sn=an+1=2n-2.
(Ⅱ)由Sn=2n-2,得bn=log2Sn=n-2,
∵cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn=1+n(n+1)(n+2)•2n-2,
cn=
+n•2n-2,
∴Tn=
+
+…+
+1×2-1+2×20+3×2+…+n•2n-2,
令A=
+
+…+
=
-
+
-
+…+
-
=
-
,
令B=1×2-1+2×2+3×21+4×22+…+(n-1)•2n-1
2B=1×20+2×21+3×22+…+(n-1)•2n-2+n•2n-1,
-B=2-1+20+2+22+…+2n-2-n•2n-1,
B=(n-1)•2n-1+
,
∴Tn=
-
+(n-1)•2n-1+
=
+(n-1)•2n-1,
当n>1时,
Tn<2n+
,即2n+
<2n+
,
∴n2+n-12>0,(n+4)(n-3)>0,n>3,
∴当n>1时,使
Tn<2n+
成立的最小正整数n的值为n=4.
当n=2时,a1+a2=a3=1,
∴a1=a2=
| 1 |
| 2 |
由
|
| an+1 |
| an |
| a2 |
| a1 |
∴数列{an}从第二项起是首项为
| 1 |
| 2 |
∴an=
|
∴Sn=an+1=2n-2.
(Ⅱ)由Sn=2n-2,得bn=log2Sn=n-2,
∵cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn=1+n(n+1)(n+2)•2n-2,
cn=
| 1 |
| (n+1)(n+2) |
∴Tn=
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n+1)(n+2) |
令A=
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n+1)(n+2) |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
令B=1×2-1+2×2+3×21+4×22+…+(n-1)•2n-1
2B=1×20+2×21+3×22+…+(n-1)•2n-2+n•2n-1,
-B=2-1+20+2+22+…+2n-2-n•2n-1,
B=(n-1)•2n-1+
| 1 |
| 2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| 2 |
| n+1 |
| n+2 |
当n>1时,
| 2 |
| n-1 |
| n+1 |
| 5 |
| 2(n+1) |
| (n-1)(n+2) |
| n+1 |
| 5 |
∴n2+n-12>0,(n+4)(n-3)>0,n>3,
∴当n>1时,使
| 2 |
| n-1 |
| n+1 |
| 5 |
点评:本题考查数列的通项公式和前n项和公式的求法,考查不等式的求法,解题时要认真审题,注意分组求和法、裂项求和法、构造法的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
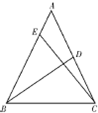 如图,在等腰三角形ABC中,底边BC=2,
如图,在等腰三角形ABC中,底边BC=2,| AD |
| DC |
| AE |
| 1 |
| 2 |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| AB |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知a、b∈R,当x>0时,不等式ax+b≥lnx恒成立,则a+b的最小值为( )
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、1 |
已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx-x,设a=f(-
),b=f(3),c=f(0),则a、b、c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<a<b |
| C、b<c<a |
| D、a<b<c |
设集合M={0,1},N={x∈Z|y=
),则( )
| 1-x |
| A、M∩N=∅ |
| B、M∩N={0} |
| C、M∩N{1} |
| D、M∩N=M |