Question

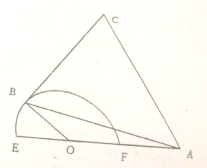如图，AO=2，B是半个单位圆上的动点，△ABC是等边三角形，求当∠AOB等于多少时，四边形OACB的面积最大，并求四边形面积的最大值．

Answer 1

考点：与圆有关的比例线段

专题：推理和证明

分析：S_{四边形OACB}=S_△AOB+S_△ABC=

1

2

•OA•OB•sinθ+

1

2

•AB•AC•sin60°=2sin（θ-

π

3

）+

5 3

4

，由此能求出四边形面积的最大值．

解答： 解：S_{四边形OACB}=S_△AOB+S_△ABC
=

1

2

•OA•OB•sinθ+

1

2

•AB•AC•sin60°
=

1

2

×1×2×sinθ+

3

4

（1+2²-2×1×2×cosθ）
=sinθ-

3

cosθ+

5 3

4

=2sin（θ-

π

3

）+

5 3

4

，
∵0＜θ＜π，∴当θ-

π

3

=

π

2

，即θ=

5π

6

时，
（S_{四边形OACB}）_max=2+

5 3

4

．

点评：本题考查当∠AOB等于多少时，四边形OACB的面积最大，并求四边形面积的最大值．解题时要注意三角形面积公式和三角函数性质的合理运用．