题目内容
在数列{an}中,a1=1,a1+
+
+…+
=2n-1(n∈N*)
(Ⅰ)求数列{an}的前n项和Sn;
(Ⅱ)若存在n∈N*,使得an≤n(n+1)λ成立,求实数λ的最小值.
| a2 |
| 2 |
| a3 |
| 3 |
| an |
| n |
(Ⅰ)求数列{an}的前n项和Sn;
(Ⅱ)若存在n∈N*,使得an≤n(n+1)λ成立,求实数λ的最小值.
考点:数列与不等式的综合
专题:综合题,不等式的解法及应用
分析:(Ⅰ)在递推式中取n取n-1得另一递推式,作差后得到数列{an}的通项公式,然后利用错位相减法求其前n项和;
(Ⅱ)把数列的通项公式代入an≤n(n+1)λ,分离参数λ后构造辅助函数f(n)=
,利用作商法得到该函数为增函数,求出函数的最小值得答案.
(Ⅱ)把数列的通项公式代入an≤n(n+1)λ,分离参数λ后构造辅助函数f(n)=
| 2n-1 |
| n+1 |
解答:
解:(Ⅰ)∵a1+
+
+…+
=2n-1 ①
∴a1+
+
+…+
=2n-1-1(n≥2)②
①-②得:
=2n-1(n≥2),
∴an=n•2n-1(n≥2).
验证n=1时成立.
∴Sn=1×20+2×21+…+(n-1)2n-2+n•2n-1
则2Sn=1×21+2×22+…+(n-1)2n-1+n•2n
两式相减得:-Sn=1+21+22+…+2n-1-n•2n=-1-(n-1)2n
∴Sn=1+(n-1)2n;
(Ⅱ)∵an=n•2n-1,
由an≤n(n+1λ,得λ≥
=
,
令f(n)=
,
∵
=
•
=
>1,
∴f(n)单调递增,
∴fmin(n)=f(1)=
,
∴λ≥
,
故λ的最小值为
.
| a2 |
| 2 |
| a3 |
| 3 |
| an |
| n |
∴a1+
| a2 |
| 2 |
| a3 |
| 3 |
| an-1 |
| n-1 |
①-②得:
| an |
| n |
∴an=n•2n-1(n≥2).
验证n=1时成立.
∴Sn=1×20+2×21+…+(n-1)2n-2+n•2n-1
则2Sn=1×21+2×22+…+(n-1)2n-1+n•2n
两式相减得:-Sn=1+21+22+…+2n-1-n•2n=-1-(n-1)2n
∴Sn=1+(n-1)2n;
(Ⅱ)∵an=n•2n-1,
由an≤n(n+1λ,得λ≥
| an |
| n(n+1) |
| 2n-1 |
| n+1 |
令f(n)=
| 2n-1 |
| n+1 |
∵
| f(n+1) |
| f(n) |
| 2n |
| n+2 |
| n+1 |
| 2n-1 |
| 2n+2 |
| n+2 |
∴f(n)单调递增,
∴fmin(n)=f(1)=
| 1 |
| 2 |
∴λ≥
| 1 |
| 2 |
故λ的最小值为
| 1 |
| 2 |
点评:本题是数列与不等式的综合题,考查了作差法求数列的通项公式,训练了利用错位相减法求数列的和,分离变量λ并构造函数是解答(Ⅱ)的关键,是中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设sinθ=
(m>0),则cos(θ+
)的取值范围是( )
| m2+1 |
| 4m |
| π |
| 6 |
A、[-1,
| ||||||
B、[-1,
| ||||||
C、[-
| ||||||
D、[-
|
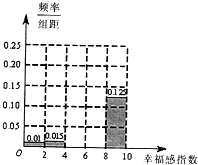 “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: