题目内容
已知函数f(x)=
+alnx(a不是0)
(Ⅰ)若a=1,求函数f(x)的极值和单调区间;
(Ⅱ) 若在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
| 1 |
| x |
(Ⅰ)若a=1,求函数f(x)的极值和单调区间;
(Ⅱ) 若在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)通过a=1,求出函数的导数,利用导数为0求出极值点,判断导函数的符号即可求解函数单调区间;
(Ⅱ) 求出函数的导数,求解极值点,转化在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,为求解函数的最值问题,利用a的取值范围的讨论,求解函数的最值,即可求得实数a的取值范围.
(Ⅱ) 求出函数的导数,求解极值点,转化在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,为求解函数的最值问题,利用a的取值范围的讨论,求解函数的最值,即可求得实数a的取值范围.
解答:
解:(I)因为f′(x)=-
+
=
,…(2分)
当a=1,f′(x)=
,令f'(x)=0,得 x=1,又f(x)的定义域为(0,+∞),f'(x),f(x)随x的变化情况如下表:
所以x=1时,f(x)的极小值为1.…(4分)f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1); …(5分)
(II)因为f′(x)=-
+
=
,且a≠0,令f'(x)=0,得到x=
,
若在(0,e]上存在一点x0,使得f(x0)<0成立,其充要条件是f(x)在区间(0,e]上的最小值小于0即可.(1)当x=
<0,即a<0时,f'(x)<0对x∈(0,+∞)成立,所以f(x)在区间(0,e]上单调递减,
故f(x)在区间(0,e]上的最小值为f(e)=
+alne=
+a,
由
+a<0,得a<-
,即a∈(-∞,-
)…(8分)
(2)当x=
>0,即a>0时,
①若e≤
,则f'(x)≤0对x∈(0,e]成立,所以f(x)在区间(0,e]上单调递减,
所以,f(x)在区间(0,e]上的最小值为f(e)=
+alne=
+a>0,
显然,f(x)在区间(0,e]上的最小值小于0不成立 …(10分)
②若0<
<e,即a>
时,则有
所以f(x)在区间(0,e]上的最小值为f(
)=a+aln
,
由f(
)=a+aln
=a(1-lna)<0,
得 1-lna<0,解得a>e,即a∈(e,+∞).
综上,由(1)(2)可知:a∈(-∞,-
)∪(e,+∞)符合题意.…(12分)
| 1 |
| x2 |
| a |
| x |
| ax-1 |
| x2 |
当a=1,f′(x)=
| x-1 |
| x2 |
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
(II)因为f′(x)=-
| 1 |
| x2 |
| a |
| x |
| ax-1 |
| x2 |
| 1 |
| a |
若在(0,e]上存在一点x0,使得f(x0)<0成立,其充要条件是f(x)在区间(0,e]上的最小值小于0即可.(1)当x=
| 1 |
| a |
故f(x)在区间(0,e]上的最小值为f(e)=
| 1 |
| e |
| 1 |
| e |
由
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
(2)当x=
| 1 |
| a |
①若e≤
| 1 |
| a |
所以,f(x)在区间(0,e]上的最小值为f(e)=
| 1 |
| e |
| 1 |
| e |
显然,f(x)在区间(0,e]上的最小值小于0不成立 …(10分)
②若0<
| 1 |
| a |
| 1 |
| e |
| x | (0,
|
| (
| ||||||
| f'(x) | - | 0 | + | ||||||
| f(x) | ↘ | 极小值 | ↗ |
| 1 |
| a |
| 1 |
| a |
由f(
| 1 |
| a |
| 1 |
| a |
得 1-lna<0,解得a>e,即a∈(e,+∞).
综上,由(1)(2)可知:a∈(-∞,-
| 1 |
| e |
点评:本题考查函数的导数的应用,考查分类讨论思想的应用,同时考查转化思想的应用.

练习册系列答案
相关题目
椭圆16x2+9y2=144长轴长是( )
| A、4 | B、3 | C、8 | D、6 |
用“二分法”求解关于x的方程lnx+2x-6=0的近似解时,能确定为解所在的初始区间的是( )
| A、(2,3) |
| B、(0,2) |
| C、(1,2) |
| D、(0,+∞) |
规定记号“⊙”表示一种运算,定义a⊙b=
+a+b(a,b为正实数),若1⊙k2<3,则k的取值范围为( )
| ab |
| A、-1<k<1 |
| B、0<k<1 |
| C、-1<k<0 |
| D、0<k<2 |
下列函数中,最小正周期为π的偶函数是( )
| A、y=sin2x | ||
B、y=cos
| ||
| C、y=sin2x+cos2x | ||
| D、y=|cosx| |
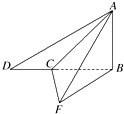 如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(
如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(