题目内容
12.在直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.(1)求圆C的参数方程;
(2)设直线y=$\sqrt{3}$x+b与圆C相切,求b的值.
分析 (1)由圆C的极坐标方程能求出圆C的普通方程,由此能求出圆C的参数方程.
(2)求出圆心C(1,0),半径r=1,由此求出圆心C(1,0)到直线$y=\sqrt{3}x+b$的距离,利用直线与圆C相切,能求出结果.
解答 解:(1)∵圆C的极坐标方程为ρ=2cosθ.
C的普通方程为(x-1)2+y2=1,
∴C的参数方程为$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$,(0≤θ<2π).
(2)由(1)知圆心C(1,0),半径r=1;
圆心C(1,0)到直线$y=\sqrt{3}x+b$的距离$d=\frac{{|{\sqrt{3}+b}|}}{2}$,
∵直线与圆C相切,∴$d=\frac{{|{\sqrt{3}+b}|}}{2}$=1,
解得$b=±2-\sqrt{3}$.
点评 本题考查圆的参数方程的求法,考查实数值的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
16.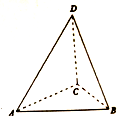 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
17.某单位招聘员工,有200名应聘者参加笔试,随机抽查了其中20名应聘者笔试试卷,统计他们的成绩如下表:
若按笔试成绩择优录取40名参加面试,由此可预测参加面试的分数线为( )
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |
17.某程序框图如图所示,对应的程序运行后输出的S的值是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
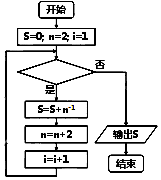

| A. | i>10 | B. | i<10 | C. | i<20 | D. | i>20 |
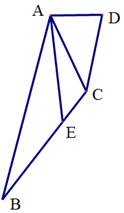 在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.