题目内容
对于定义域为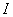 的函数
的函数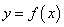 ,如果存在区间
,如果存在区间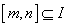 ,同时满足:①
,同时满足:①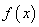 在
在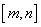 内是单调函数;②当定义域是
内是单调函数;②当定义域是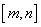 ,
,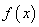 值域也是
值域也是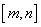 ,则称
,则称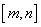 是函数
是函数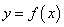 的“好区间”.
的“好区间”.
(Ⅰ)设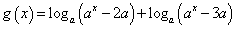 (其中
(其中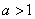 ),判断
),判断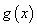 是否存在“好区间”,并说明理由;
是否存在“好区间”,并说明理由;
(Ⅱ)已知函数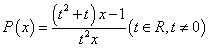 有“好区间”
有“好区间”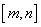 ,当
,当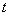 变化时,求
变化时,求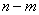 的最大值.
的最大值.
(1)由 .……………………………………1分
.……………………………………1分
①当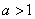 时,
时, ,此时定义域
,此时定义域 ,
, ,
, ,
,
 ,
, ,
, ,
,
 ,
, ,
,
 ,
,
 在
在 内是增函数; 3分
内是增函数; 3分
 存在“好区间”
存在“好区间”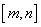
 ,
,
 关于
关于 的方程
的方程 在定义域
在定义域 内有两个不等的实数根.
内有两个不等的实数根.
即 在定义域
在定义域 内有两个不等的实数根.(*)
内有两个不等的实数根.(*)
设 ,则(*)
,则(*)
 ,
,
即 在
在 内有两个不等的实数根,
内有两个不等的实数根,
设 ,则
,则 无解.
无解.
所以函数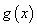 不存在“好区间”. ……………………………………6分
不存在“好区间”. ……………………………………6分
(2)由题设,函数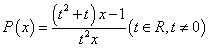 有“好区间”
有“好区间”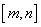 ,
,
 或
或 ,函数
,函数 在
在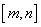 上单调递增,
上单调递增,
 ,所以
,所以 是方程
是方程 ,即方程
,即方程 有同号的相异实数根.
有同号的相异实数根.
 ,
, 同号,
同号, 或
或 .
.
 ,
, .
.
当 ,
,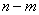 取得最大值
取得最大值 .
.

练习册系列答案
相关题目
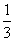 ,某植物研究所进行该种子的发芽实验,每
,某植物研究所进行该种子的发芽实验,每 次实验种一粒种子, 每次实验结果相互独立. 假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设
次实验种一粒种子, 每次实验结果相互独立. 假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设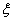 表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.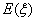 ;
;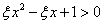 的解集是实数集R”为事件A,求事件A发生的概率
的解集是实数集R”为事件A,求事件A发生的概率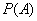 .
. ,不等式
,不等式 ,
, ,
, ,…,可推广为
,…,可推广为 ,则
,则 等于 .
等于 . 的左、右焦点分别为F1、F2,以F1F2为直径的圆被直线
的左、右焦点分别为F1、F2,以F1F2为直径的圆被直线 截得的弦长为
截得的弦长为 a,则双曲线的离心率为( )
a,则双曲线的离心率为( ) D.
D.
 ,对任意的
,对任意的 ,恒有
,恒有 成立,则实数a的取值范围是 .
成立,则实数a的取值范围是 . ,
, ,则△ABC的面积为(
,则△ABC的面积为(  ).
). B.3 C.
B.3 C. D.6
D.6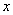 的不等式
的不等式 的解集为R, 则
的解集为R, 则 的取值范围是 .
的取值范围是 .  , 则输出
, 则输出
 的值为
的值为 B.
B. C.
C. D.
D.

 (
( ,则“
,则“ ”是“函数
”是“函数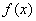 为奇函数”的 条件(用“充分不必要”,“必要不充分”“充要”“既非充分又非必要”)
为奇函数”的 条件(用“充分不必要”,“必要不充分”“充要”“既非充分又非必要”)