题目内容
关于x的方程x2-mx+m+1=0(k∈R)的两实根为sinθ和cosθ,θ∈(0,2π),sinθ+cosθ求:
(1)m的值;
(2)
+
的值;
(3)方程的两实根及此时θ的值.
(1)m的值;
(2)
| sinθ | ||
1+
|
| cosθ |
| 1+tanθ |
(3)方程的两实根及此时θ的值.
考点:三角函数的恒等变换及化简求值,根与系数的关系
专题:三角函数的求值
分析:(1)利用韦达定理可求得m2-2m-3=0,解得m=-1或m=3(舍去),从而可得m的值;
(2)由(1)知m=-1,将所求的关系式化简为
,将m=-1代入即可求得答案;
(3)由m=-1,知sinθ+cosθ=-1,sinθ•cosθ=-1+1=0,而θ∈(0,2π),从而可得方程的两实根及此时θ的值.
(2)由(1)知m=-1,将所求的关系式化简为
| 1 |
| m |
(3)由m=-1,知sinθ+cosθ=-1,sinθ•cosθ=-1+1=0,而θ∈(0,2π),从而可得方程的两实根及此时θ的值.
解答:
解:(1)∵为sinθ和cosθ为方程x2-mx+m+1=0(k∈R)的两实根,
∴sinθ+cosθ=m,sinθ•cosθ=m+1,
∵(sinθ+cosθ)2=sin2θ+2sinθcosθ+cos2θ=1+2sinθcosθ,
∴m2=1+2(m+1),即m2-2m-3=0,
解得:m=-1或m=3(舍去),
∴m=-1.
(2)由(1)知m=-1,
∴原式=
+
=
=
=
=-1;
(3)∵sinθ+cosθ=-1,sinθ•cosθ=-1+1=0,
∴sinθ=0,cosθ=-1或cosθ=0,sinθ=-1,
又θ∈(0,2π),
∴θ=π或θ=
.
∴sinθ+cosθ=m,sinθ•cosθ=m+1,
∵(sinθ+cosθ)2=sin2θ+2sinθcosθ+cos2θ=1+2sinθcosθ,
∴m2=1+2(m+1),即m2-2m-3=0,
解得:m=-1或m=3(舍去),
∴m=-1.
(2)由(1)知m=-1,
∴原式=
| sinθ | ||
1+
|
| cosθ | ||
1+
|
| sin2θ+cos2θ |
| sinθ+cosθ |
| 1 |
| sinθ+cosθ |
| 1 |
| m |
(3)∵sinθ+cosθ=-1,sinθ•cosθ=-1+1=0,
∴sinθ=0,cosθ=-1或cosθ=0,sinθ=-1,
又θ∈(0,2π),
∴θ=π或θ=
| 3π |
| 2 |
点评:本题考查三角函数的恒等变换及化简求值,考查根与系数的关系,着重考查韦达定理的应用与正弦函数与余弦函数的性质,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、任何事件的概率总是在(0,1)之间 |
| B、频率是客观存在的,与试验次数无关 |
| C、随着试验次数的增加,频率一般会越来越接近概率 |
| D、概率是随机的,在试验前不能确定 |
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,等式m+n+c=0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
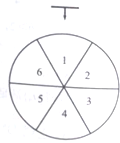 商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.
商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.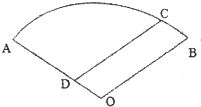 吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).