题目内容
已知函数f(x)=ex-a(x+2)-b(e为自然对数的底,a,b∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)的最小值为0,求b的最大值.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)的最小值为0,求b的最大值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)先对函数求导,令导函数大于0得到递增区间,令导函数小于0得到递减区间;
(2)函数f(x)的最小值为0求出b的值,令h(x)=-x-lnx,求出 h′(x).判断h(x)的单调性,求极值点,继而得到答案.
(2)函数f(x)的最小值为0求出b的值,令h(x)=-x-lnx,求出 h′(x).判断h(x)的单调性,求极值点,继而得到答案.
解答:
解:(1)f'(x)=ex-a,
若a≤0,则f'(x)≥0恒成立,则f(x)在区间(-∞,+∞)上是单调递增;
若a>0,由f'(x)>0解得x>lna,
f(x)在区间(lna,+∞)上单调递增,在区间(-∞,lna)上单调递减.
(2)若a≤0,则f'(x)≥0恒成立,则f(x)在区间(-∞,+∞)上单调递增,函数f(x)不存在最小值;
若a>0,由(1)f(x)在区间(lna,+∞)上单调递增,在区间(-∞,lna)上单调递减,
∴函数f(x)的最小值是f(lna)=a-a(lna+2)-b,因此b=-a-alna,
记h(x)=-x-xlnx,h′(x)=-1-lnx-x•
=-lnx-2,
由h'(x)=0⇒x=e-2,
且当0<x<e-2时,h'(x)>0,
且当x>e-2时,h'(x)<0,
所以h(x)的最大值是h(e-2)=e-2,即b的最大值是e-2.
若a≤0,则f'(x)≥0恒成立,则f(x)在区间(-∞,+∞)上是单调递增;
若a>0,由f'(x)>0解得x>lna,
f(x)在区间(lna,+∞)上单调递增,在区间(-∞,lna)上单调递减.
(2)若a≤0,则f'(x)≥0恒成立,则f(x)在区间(-∞,+∞)上单调递增,函数f(x)不存在最小值;
若a>0,由(1)f(x)在区间(lna,+∞)上单调递增,在区间(-∞,lna)上单调递减,
∴函数f(x)的最小值是f(lna)=a-a(lna+2)-b,因此b=-a-alna,
记h(x)=-x-xlnx,h′(x)=-1-lnx-x•
| 1 |
| x |
由h'(x)=0⇒x=e-2,
且当0<x<e-2时,h'(x)>0,
且当x>e-2时,h'(x)<0,
所以h(x)的最大值是h(e-2)=e-2,即b的最大值是e-2.
点评:本题考查导数知识的运用,考查利用导数研究函数的单调性,极值及最值,要注意求极值时,导数等于0根的左右单调性的判断.考查了分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若“m≤a”是“方程x2+x+m=0有实根”的必要不充分条件,则实数a的取值范围是( )
A、a≤
| ||
B、a<
| ||
C、a≥
| ||
D、a>
|
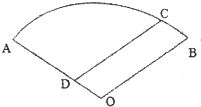 吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).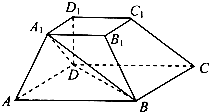 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.