题目内容
6.等比数列$\left\{{a_n}\right\}满足:{a_1}=b-1(b>0且b≠1),{S_2}={b^2}-1$.(1)求数列{an}的通项公式;
(2)当b=2时,记${b_n}=\frac{n+1}{{4{a_n}}}$,求数列{bn}的前n项和Tn.
分析 (1)由已知求出a2,进一步得到公比,则数列{an}的通项公式可求;
(2)把数列{an}的通项公式代入${b_n}=\frac{n+1}{{4{a_n}}}$,利用错位相减法求数列{bn}的前n项和Tn.
解答 解:(1)∵a1=b-1,${S}_{2}={b}^{2}-1$,
∴${a}_{1}+{a}_{2}=b-1+{a}_{2}={b}^{2}-1$,则${a}_{2}={b}^{2}-b$,
又数列{an}是等比数列,∴公比q=$\frac{{a}_{2}}{{a}_{1}}=\frac{{b}^{2}-b}{b-1}=b$.
∴${a}_{n}=(b-1)•{b}^{n-1}$;
(2)当b=2时,${a}_{n}={2}^{n-1}$,
则${b_n}=\frac{n+1}{{4{a_n}}}$=$\frac{n+1}{{2}^{n+1}}$.
∴Tn=$\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+\frac{4}{{2}^{4}}+…+\frac{n}{{2}^{n}}+\frac{n+1}{{2}^{n+1}}$,
则$\frac{{T}_{n}}{2}=\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n}{{2}^{n+1}}+\frac{n+1}{{2}^{n+2}}$,
两式作差可得:$\frac{1}{2}{T}_{n}=\frac{1}{2}+(\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n+1}})-\frac{n+1}{{2}^{n+2}}$=$\frac{1}{2}+\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}-\frac{n+1}{{2}^{n+2}}$.
∴${T}_{n}=\frac{3}{2}-\frac{n+3}{{2}^{n+1}}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,是中档题.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
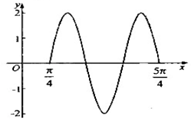 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).